Question

Three identical rods, each of length l, are joined to form a rigid equilateral triangle. Its radius of gyration about an axis passing through a corner and perpendicular to the plane of the triangle is
A. \[\dfrac{l}{2}\]
B. \[\sqrt{\dfrac{3}{2}}l\]
C. \[\dfrac{l}{\sqrt{2}}\]
D. \[\dfrac{l}{\sqrt{3}}\]

Answer 1

Hint: In this question we are asked to calculate the radius of gyration about an axis passing through one of corner points and perpendicular to the plane of triangle. Therefore, we will be calculating the moment of inertia of all the rods about the given point. Later, we will calculate the radius of gyration by using the formula that states the relation between total moment of inertia and radius of gyration.
Formula Used:
\[M{{k}^{2}}={{I}_{t}}\]
Where,
\[{{I}_{t}}\] is the total moment of inertia about point
k is the radius of gyration
M is the total mass of system

Complete answer:
It is given that three rods of equal length form a rigid equilateral triangle as shown in the figure below.

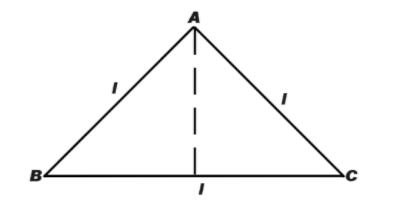
We know that radius of gyration is given by,
\[M{{k}^{2}}={{I}_{t}}\] ………………….. (A)
Therefore, we need to calculate the value of \[{{I}_{t}}\]. To calculate it we will first calculate the moment of inertia of each individual rod.
We know, that rods AB and AC are similar in every way as they form sides of equilateral triangle
Therefore, the moment of inertia of Ab will be equal to AC.
We know that MOI about an endpoint is given as \[\dfrac{m{{l}^{2}}}{3}\]
Therefore,
\[{{I}_{AB}}={{I}_{AC}}=\dfrac{m{{l}^{2}}}{3}\]
MOI for BC, we will be using parallel axis theorem
Therefore,
\[{{I}_{BC}}=\dfrac{m{{l}^{2}}}{12}+m{{r}^{2}}\] ………………….. (2)
From the figure, we can say
\[{{r}^{2}}={{l}^{2}}-\dfrac{{{l}^{2}}}{4}\] …………………. (Pythagoras theorem)
Therefore,
\[{{r}^{2}}={{\dfrac{3l}{4}}^{2}}\]
After substituting the value of r in equation (2)
We get,
\[{{I}_{BC}}=\dfrac{m{{l}^{2}}}{12}+m{{\dfrac{3l}{4}}^{2}}\]
Therefore,
\[{{I}_{BC}}=\dfrac{10m{{l}^{2}}}{12}\]
Now,
\[{{I}_{t}}={{I}_{AB}}+{{I}_{AC}}+{{I}_{BC}}\]
Substitute values from (1) and (2)
We get,
\[{{I}_{t}}=\dfrac{m{{l}^{2}}}{3}+\dfrac{10m{{l}^{2}}}{12}\]
Therefore,
\[{{I}_{t}}=\dfrac{3m{{l}^{2}}}{2}\]
The total mass of system is 3m
Substituting these values in (A)
We get,
\[3m{{k}^{2}}={{I}_{t}}\]
Therefore,
\[{{k}^{2}}=\dfrac{3m{{l}^{2}}}{2}\times \dfrac{1}{3m}\]
On solving,
\[{{k}^{2}}=\dfrac{{{l}^{2}}}{2}\]
Therefore, the radius of gyration
\[k=\dfrac{l}{\sqrt{2}}\]

Therefore, the correct answer is option C.

Note:
Radius of gyration is the distance from the given axis at which the mass of the body can be assumed to be concentrated and at which the moment of inertia would be equal to the moment of inertia of the original mass about the axis. Moment of inertia is a quantity that determines the torque needed for the angular acceleration of the object about the rotational axis.