Question

There is a small island in the middle of a 100m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks and in line with the tree. If the angle of elevation of the top of the tree from P and Q are respectively ${\text{30}^\circ }$ and ${\text{45}^\circ }$, find the height of the tree.

Answer 1

Hint: We can draw a diagram and get 2 right angles triangles. In these triangles, we can find 2 trigonometric ratios with the height of the tree and distance from its bottom to the point. We can solve the two equations to get the height of the tree.

Complete step by step solution: We can draw a diagram to get a better understanding of the question.

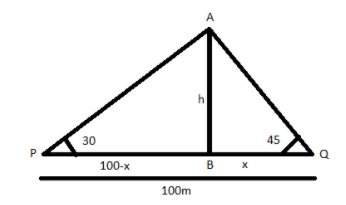
Let AB be the tree and h is the height of the tree. Let x be the distance to the bottom of the tree from point Q. Then the distance to point p from the tree is ${\text{100 - x}}$.
Consider triangle ABQ,
$\tan \left( Q \right) = \dfrac{{AB}}{{BQ}}$
$ \Rightarrow \tan \left( {{{45}^{\text{o}}}} \right) = \dfrac{h}{x}$
We know that $\tan \left( {{{45}^{\text{o}}}} \right) = 1$, so we get,
$1 = \dfrac{h}{x}$ …. (1)

Consider triangle ABP,
${\text{tan}}\left( {\text{P}} \right){\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{BP}}}}$
${\text{tan}}\left( {{\text{3}}{{\text{0}}^{\text{o}}}} \right){\text{ = }}\dfrac{{\text{h}}}{{{\text{100 - x}}}}$
We know that ${\text{tan}}\left( {{\text{3}}{{\text{0}}^{\text{o}}}} \right){\text{ = }}\dfrac{{\text{1}}}{{\sqrt {\text{3}} }}$, so we get,
$\dfrac{1}{{\sqrt 3 }}{\text{ = }}\dfrac{{\text{h}}}{{{\text{100 - x}}}}$
$ \Rightarrow {\text{100 - x = h}}\sqrt {\text{3}} $… (2)
Substituting equation (1) in (2), we get,
$
  {\text{100 - h = h}}\sqrt {\text{3}} \\
  {\text{h}}\sqrt {\text{3}} {\text{ + h = 100}} \\
  \left( {\sqrt {\text{3}} {\text{ + 1}}} \right){\text{h = 100}} \\
 $
$ \Rightarrow {\text{h = }}\dfrac{{{\text{100}}}}{{\sqrt {\text{3}} {\text{ + 1}}}}{\text{m}}$

Therefore, height of the tree is $\dfrac{{{\text{100}}}}{{\sqrt {\text{3}} {\text{ + 1}}}}{\text{m}}$.

Note: Drawing a diagram is helpful for a better understanding of the question. We can also find the distance to the base of the tree from the points P and Q by finding the value of x. The concept of trigonometry is used here. The trigonometric relation used in this problem is ${\tan \theta = }\dfrac{{{\text{opposite side}}}}{{{\text{adjecent side}}}}$ . We must be careful while taking the angles and sides. The angle of elevation decreases as we go away from the base of the tree.