Question

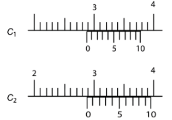
There are two Vernier callipers both of which have $1\,cm$ divided into $10$ equal divisions on the main scale. The vernier scale of one of the callipers $({C_1})$ has $10$ equal divisions that correspond to $9$ main scale divisions. The vernier scale of the other calliper $({C_2})$ has $10$ equal divisions that correspond to $11$ main scale divisions. The readings of the two callipers are shown in the figure. The measured values (in $cm$) by callipers ${C_1}$ and ${C_2}$ respectively are:

(A) $2.87$ and $2.87$
(B) $2.87$ and $2.83$
(C) $2.85$ and $2.82$
(D) $2.87$ and $2.86$

Answer 1

Hint: A vernier calliper is a measuring instrument consisting of a main scale with a fixed jaw and a moving jaw with a vernier attached. Here we have to first find the vernier scale division and then the main scale division to calculate the reading.

Complete step by step answer:
The vernier calliper least count function is determined by dividing the smallest reading of the main scale by the total number of vernier scale divisions.
For any form of scale the least count is an important determining parameter. Least count of vernier callipers is the difference between one smallest main scale reading and one smallest vernier scale reading which is $0.1\,mm$ or $0.01\,cm$. The least count is therefore important since it is specifically related to an instrument’s precision, and in some situations precision and least count are used interchangeably while they have separate definitions.
For a calliper if the least count is known, then we can use the following formula to conveniently find any length-
Length=MSR + (VSR×L.C)
Where MSR=main scale reading
VSR=Vernier scale reading and
L.C= least count
Now we can find the solution-
MSD $ = \dfrac{1}{{10}}\,cm = 0.1\,cm$
For first vernier calliper, $10$ VSD $ = 9$ MSD
VSD $ = \dfrac{9}{{10}}$
MSD $ = 0.9 \times 0.1 = 0.09\,cm$
Reading = main scale reading up to coinciding main scale division $ - n \times $ VSD = $3.5 - 7 \times 0.09 = 3.5 - 0.63 = 2.87\,cm$
For second vernier calliper, $10$ VSD$ = 11$ MSD
VSD $ = \dfrac{{11}}{{10}}$
MSD $ = 1.1 \times 0.1 = 0.11\,cm$
Reading $ = 3.6 - 7 \times 0.11 = 3.6 - 0.77 = 2.83\,cm$
Hence, option (B) is the correct answer.

Note:While taking reading on a vernier scale we should check the alignment of the main scale and the vernier scale. There may still be error due to the human eye. So, the main scale reading formula helps in overcoming these errors and least count helps in overcoming these errors.