Question

There are two towers, one on each bank of a river, just opposite to each other, one tower is 50 m high. From the top of this tower, the angles of depressions of the top and foot of the other tower are ${{30}^{\circ }}\And {{60}^{\circ }}$ respectively. Find the width of the river and the height of the other tower.

Answer 1

Hint: First of all draw the diagram according to the requirements of the above question. Then we will get different measurements of right-angled triangles. Then we are going to use the following trigonometric ratio in different right triangles to evaluate the width of the river and height of the tower, $\tan \theta =\dfrac{P}{B}$. In this formula, “P” represents the perpendicular and “B” represents the base of the right triangle with respect to angle $\theta $.

Complete step-by-step solution:
In the below diagram, we have shown the tower of length 50 m as AB and draw the angle of depressions as ${{30}^{\circ }}\And {{60}^{\circ }}$ from point A to the top (which is point C) and bottom (which is point D) to the other tower.

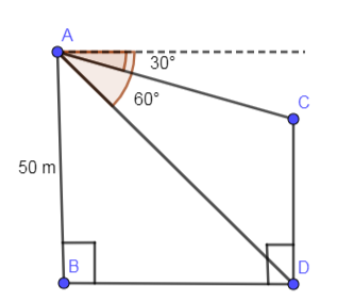
            Figure (1)
Let us assume that the width of the river is “w” and the height of the other tower be “h”. Marking these lengths in the above diagram we get,

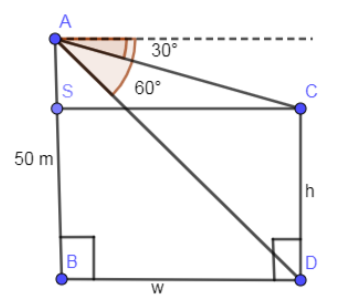
               Figure (2)
In the above diagram, the value of angle ACS is equal to ${{30}^{\circ }}$ from the alternate interior angles. Similarly, angle ADB is equal to ${{60}^{\circ }}$. Marking these angles in the above diagram we get,

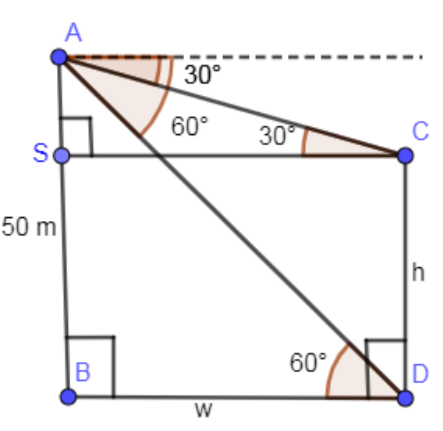
                    Figure (3)
Now, in the right-angled triangle ABD, we are going to apply the trigonometric ratio $\tan \theta =\dfrac{P}{B}$ where “P” represents perpendicular and “B” represents the base of the right triangle with respect to angle $\theta $.
To get more clarity about this trigonometric ratio, we have shown a right triangle PQR with angle $\theta $ and PQ as “P” and QR as “B”.
 

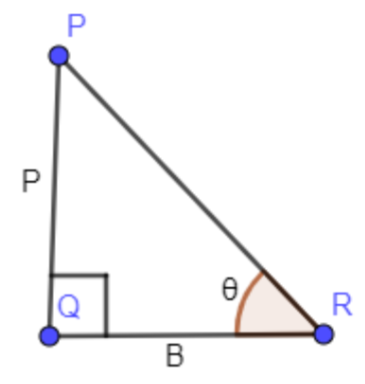
Applying $\tan \theta $ in the above right triangle PQR we get,
$\tan \theta =\dfrac{P}{B}$
Applying $\tan {{60}^{\circ }}$ in the right triangle ABD of figure (3) we get,
$\tan {{60}^{\circ }}=\dfrac{AB}{BD}$
Substituting AB as 50 m and BD as “w” in the above equation we get,
$\begin{align}
  & \tan {{60}^{\circ }}=\dfrac{50}{w} \\
 & \Rightarrow \sqrt{3}=\dfrac{50}{w} \\
\end{align}$
Rearranging the above equation we get,
$w=\dfrac{50}{\sqrt{3}}$
Rationalizing the above equation by multiplying and dividing the R.H.S of the above equation by $\sqrt{3}$ we get,
$\begin{align}
  & w=\dfrac{50}{\sqrt{3}}\times \dfrac{\sqrt{3}}{\sqrt{3}} \\
 & \Rightarrow w=\dfrac{50\sqrt{3}}{3}m \\
\end{align}$
As we have assumed “w” as the width of the river so we are getting the width of the river as $\dfrac{50\sqrt{3}}{3}m$.
Applying $\tan {{30}^{\circ }}$ in right triangle ASC shown in figure (3) we get,
$\tan {{30}^{\circ }}=\dfrac{AS}{SC}$
Now, SC is equal to BD which is equal to “w” so substituting SC as “w” in the above equation we get,
$\begin{align}
  & \tan {{30}^{\circ }}=\dfrac{AS}{w} \\
 & \Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{AS}{w} \\
\end{align}$
Multiplying “w” on both the sides we get,
$\dfrac{w}{\sqrt{3}}=AS$
As we have calculated the value of “w” as $\dfrac{50\sqrt{3}}{3}m$ so substituting this value of “w” in the above equation we get,
$\begin{align}
  & \dfrac{50\sqrt{3}}{3\sqrt{3}}=AS \\
 & \Rightarrow AS=\dfrac{50}{3}m \\
\end{align}$
Now, look at the figure (3),

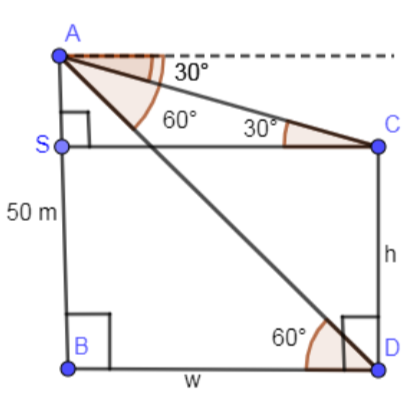
If you carefully look at the above figure, you will find that the length of AB is equal to the sum of sides AS and SB.
\[AB=AS+SB\]
From the figure, SB is equal to CD and we have assumed the length of CD as “h” so the length of SB becomes “h”.
Substituting SB as h, AB as 50 m and AS as $\dfrac{50}{3}m$ in \[AB=AS+SB\] we get,
\[\begin{align}
  & 50=\dfrac{50}{3}+h \\
 & \Rightarrow h=50-\dfrac{50}{3} \\
 & \Rightarrow h=50\left( 1-\dfrac{1}{3} \right) \\
 & \Rightarrow h=50\left( \dfrac{2}{3} \right) \\
 & \Rightarrow h=\dfrac{100}{3}m \\
\end{align}\]
Hence, we got the value of “h” as $\dfrac{100}{3}m$ which we have assumed as the height of the other tower.
Hence, we got the width of the river as $\dfrac{50\sqrt{3}}{3}m$ and the height of the other tower as $\dfrac{100}{3}m$.

Note: The question demands the good knowledge of the trigonometric ratios and what is the angle of depression means and some basic geometry. The basic geometry that we have used above is alternate interior angles. If you miss any of these concepts then you will be paralyzed in this problem.
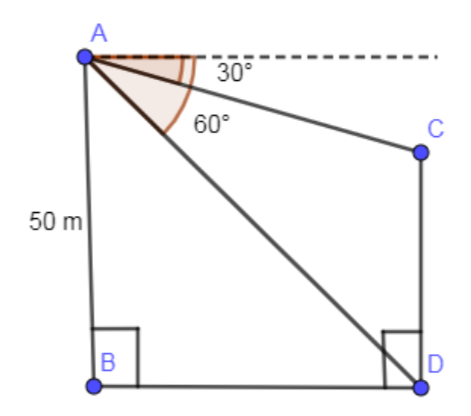
One more thing, students generally get confused with the angle of depression. The angle of depression is always made from the horizontal axis to the line of sight of the observer to the object and angle of depression made only when the observer is looking downwards which you can verify yourself from the below diagram.