Question

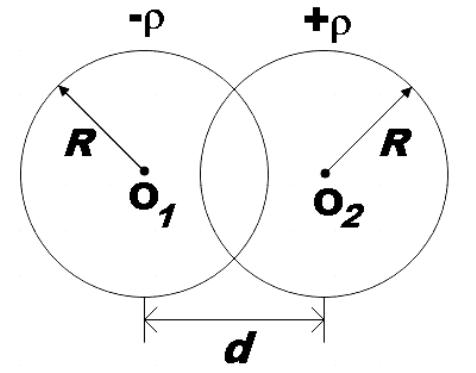
There are two non conducting spheres having uniform volume charge densities $\rho $ and $-\rho $. Both spheres have equal radius R. The spheres are now laid down such that they overlap as shown in the figure. The electric field $\overrightarrow{E}$ in the overlap region is:

A. non uniform
B. zero
C. $\dfrac{\rho }{3{{\varepsilon }_{0}}}\overrightarrow{d}$
D.$\dfrac{\rho }{3{{\varepsilon }_{0}}}\overrightarrow{r}$

Answer 1

Hint: Recall the expression for electric field due to a non-conducting sphere with charge density $\rho $. Now consider a point P in the overlapping region of the given two spheres and then find the electric field due to each sphere at that particular point. Now their sum will give you the net field in that region and hence the answer.

Formula used:
Electric field inside a non-conducting sphere at distance r,
$E=\dfrac{\rho \overrightarrow{r}}{3{{\varepsilon }_{0}}}$

Complete answer:
In the question we are given two non conducting spheres of equal radius with uniform charge densities $-\rho $ and $+\rho $. These spheres are laid down as shown in the figure and from which we could see that they overlap each other. We are asked to find the electric field in the overlapped region.
Firstly let us recall the expression for electric field at a point inside the sphere at a vector distance $\overrightarrow{r}$ from the centre.
$E=\dfrac{Q}{4\pi {{\varepsilon }_{0}}}\dfrac{\overrightarrow{r}}{{{R}^{3}}}$
Where, Q is the charge of the sphere. But we know that the volume charge density $\rho $ of a sphere is given by,
$\rho =\dfrac{Q}{\dfrac{4}{3}\pi {{R}^{3}}}$
$\Rightarrow Q=\dfrac{4}{3}\pi {{R}^{3}}\rho $
Substituting this in the expression for electric field we get,
$E=\dfrac{\left( \dfrac{4}{3}\pi {{R}^{3}}\rho \right)}{4\pi {{\varepsilon }_{0}}}\dfrac{\overrightarrow{r}}{{{R}^{3}}}$
$\Rightarrow E=\dfrac{\rho \overrightarrow{r}}{3{{\varepsilon }_{0}}}$ …………………………………… (1)
Now let us consider a point P in the overlapped region at a distance $\overrightarrow{{{r}_{1}}}$ from the centre of the first sphere and $\overrightarrow{{{r}_{2}}}$ from the centre of second sphere.

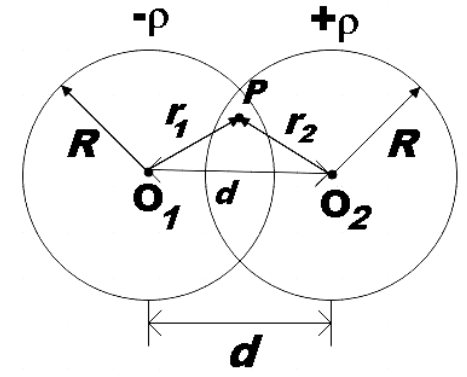
Now the electric field at P due to sphere charge density $-\rho $ will be,
${{E}_{1}}=\dfrac{-\rho \overrightarrow{{{r}_{1}}}}{3{{\varepsilon }_{0}}}$
Now the electric field at P due to sphere charge density $\rho $will be,
${{E}_{2}}=\dfrac{\rho \overrightarrow{{{r}_{2}}}}{3{{\varepsilon }_{0}}}$
Net field at P will be,
$E={{E}_{1}}+{{E}_{2}}$
$E=\dfrac{-\rho \overrightarrow{{{r}_{1}}}}{3{{\varepsilon }_{0}}}+\dfrac{\rho \overrightarrow{{{r}_{2}}}}{3{{\varepsilon }_{0}}}$
$E=\dfrac{\rho }{3{{\varepsilon }_{0}}}\left( \overrightarrow{{{r}_{2}}}-\overrightarrow{{{r}_{1}}} \right)$
But from the figure,
$\overrightarrow{d}=\overrightarrow{{{r}_{2}}}-\overrightarrow{{{r}_{1}}}$
Therefore, the electric field in the overlapping region will be,
$E=\dfrac{\rho }{3{{\varepsilon }_{0}}}\overrightarrow{d}$

Hence, the answer to the given question is option C.

Note:
The difference between a conducting and non-conducting sphere is that the charge is present only on the surface for a conducting sphere but for a non-conducting sphere, it is uniformly distributed. Due to the same reason, the electric field due to both spheres will be very different. The direction of the electric field will be perpendicularly outward.