Question

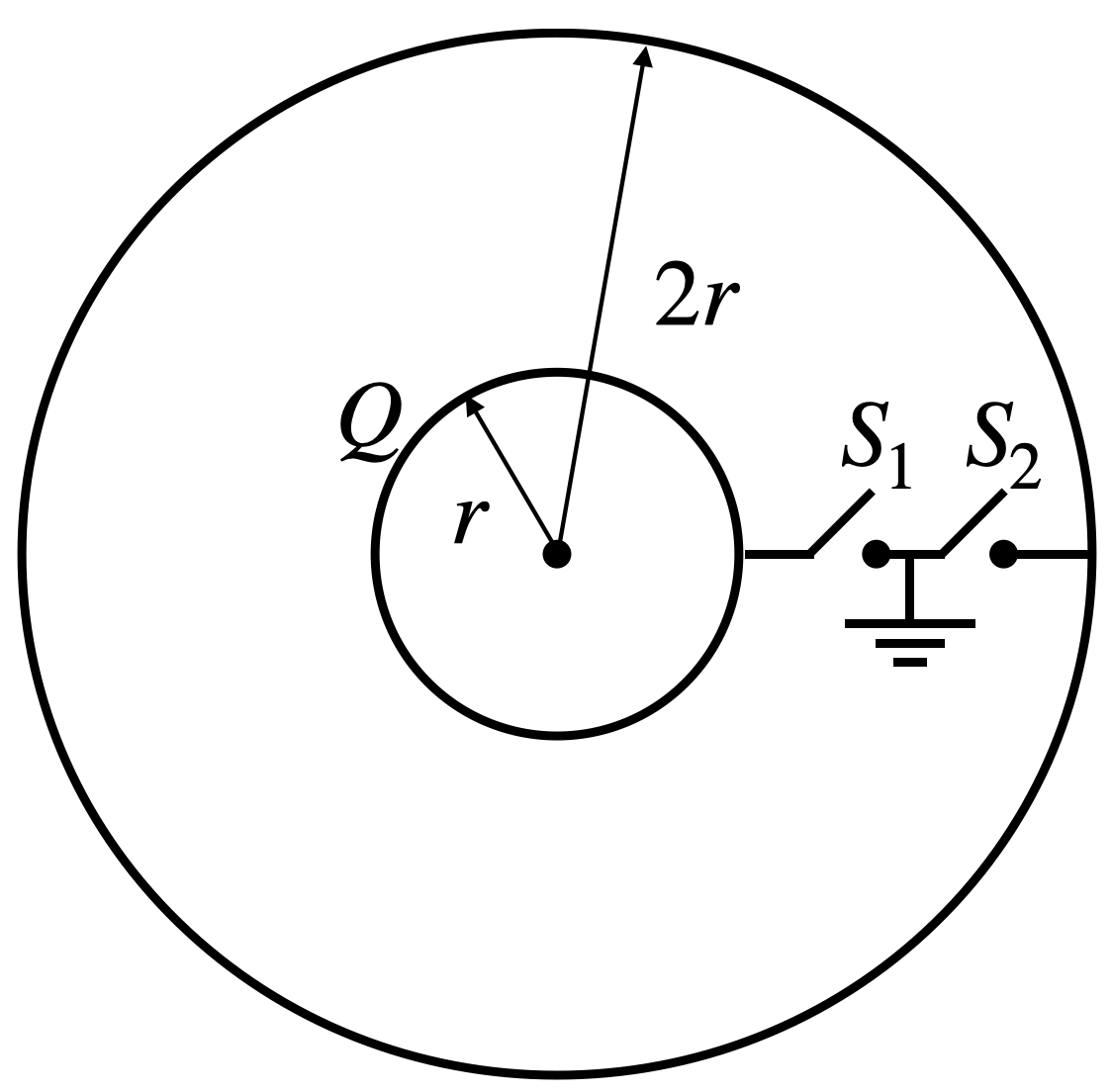
There are two concentric spherical shells of radii r and 2r. Initially, a charge Q is given to the inner shell. Now, switch ${{S}_{2}}$ is closed and opened then ${{S}_{1}}$ is closed and opened, and the process is repeated n times for both the keys alternatively. Find the final potential difference between shells.

Answer 1

Hint: Calculate the potential at the surface of the outer sphere and equate it with zero when it is connected to the ground. When the inner sphere is connected to the ground, find the potential at the surface of the inner sphere and equate with zero. Find a trend in the charge after each iteration. Remember that potential inside a spherical shell remains the same as of the potential at the surface.
Formula Used:
The potential outside a spherical shell is given by,
$U=-\dfrac{kQ}{r}$....................(1)
The potential inside a spherical shell is given by,
$U=-\dfrac{kQ}{R}$.....................(2)
Where,
$Q$ is the charge of the sphere
$k$ is the Coulomb’s constant
$r$ is the distance from the centre
$R$ is the radius of the sphere.

Complete step-by-step answer:
When we connect the spherical shell to ground the charge on the grounded shell will organize such that the potential of the shell is zero.
Let’s assume that after closing ${{S}_{2}}$ the charge on the outer shell is,
${{q}_{1}}$
Hence, the potential at the surface of the outer sphere due to the outer sphere charge is given by equation (1),
${{U}_{1}}=-\dfrac{k{{q}_{1}}}{2r}$
Now, the potential at the surface of the outer sphere due to the inner is given by equation (1),
${{U}_{1}}=-\dfrac{kQ}{2r}$

Hence, the total potential is,
$U={{U}_{1}}+{{U}_{2}}=-(\dfrac{kQ}{2r}+\dfrac{k{{q}_{1}}}{2r})$
This potential should be zero, as it is connected to the ground.
Hence, we can write,
$0=-(\dfrac{kQ}{2r}+\dfrac{k{{q}_{1}}}{2r})$
$\Rightarrow {{q}_{1}}=-Q$
So,
${{q}_{1}}=-Q$
Now, when we close ${{S}_{1}}$, let’s assume the charge at the inner sphere is,
$q_{1}^{'}$
The potential due to the outer sphere at the surface of the inner sphere is given by Equation (2),
$U_{1}^{'}=-\dfrac{k(-Q)}{2r}=\dfrac{kQ}{2r}$
The potential due to the inner sphere at the same location is given by equation (1),
$U_{2}^{'}=-\dfrac{kq_{1}^{'}}{r}$
So, we can similarly write,
$U=U_{1}^{'}+U_{2}^{'}=\dfrac{kQ}{2r}-\dfrac{kq_{1}^{'}}{r}$
$\Rightarrow 0=\dfrac{kQ}{2r}-\dfrac{kq_{1}^{'}}{r}$
$\Rightarrow q_{1}^{'}=\dfrac{Q}{2}$
Now, again after closing ${{S}_{2}}$ we can write,
$\dfrac{k(\dfrac{Q}{2})}{2r}+\dfrac{k{{q}_{2}}}{2r}=0$
$\Rightarrow {{q}_{2}}=-\dfrac{Q}{2}$

After closing ${{S}_{1}}$ we can write,
$\dfrac{kQ}{2\times 2r}-\dfrac{kq_{2}^{'}}{r}=0$
$\Rightarrow q_{2}^{'}=\dfrac{Q}{4}$

So, this follows a geometric progression.
Hence, after n times, the charge will be,
${{q}_{n}}=-\dfrac{Q}{{{2}^{n-1}}}$
$q_{n}^{'}=\dfrac{Q}{{{2}^{n}}}$

Hence the potential difference will be,
$V=kq_{n}^{'}(\dfrac{1}{r}-\dfrac{1}{2r})=\dfrac{kQ}{{{2}^{n+1}}r}$

Note:
You may have noticed that the potential inside a sphere and the potential at the surface has the same value. It is a direct consequence of Gauss's Law. As there is no charge inside the sphere, there is no electric field inside the spherical cavity. As a result, the potential remains the same. You don’t need to perform any work to move a charged particle inside a sphere.