
There are triangles $ \Delta DEC $ and $ \Delta BEF $ and a parallelogram ABCD in the given figure. Use the congruence property of triangles to prove CD=BF . We get from the parallelogram CD=AB. Then we use the given information AF=2AB in the question to proceed.

Answer
573k+ views
Hint: There are triangles and a parallelogram in the given figure. Use the congruence property of triangles to prove CD=AB and parallelogram as well as the given information in the question to proceed.
Complete step-by-step answer:
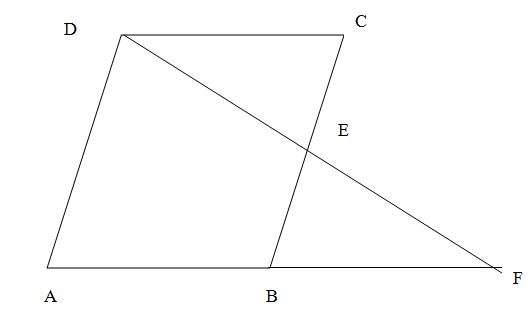
We see in the given figure that ABCD is a parallelogram which means the opposite sides are of equal length and opposite angles are of equal measurement. Mathematically,
\[AB=CD,AD=BC,\angle ADC=\angle ABC,\angle BAC=BCD\]
We are also given in the question that E is the midpoint of BC which means $ BE=CE $ . When DE and AB are extended they meet on a point F. We are asked to prove $ \text{AF}=\text{2AB} $ .\[\]
Let us observe the two triangles $ \Delta DEC $ and $ \Delta BEF $ . We see that the angles $ \angle DEC $ and $ \angle BEF $ are vertically opposite to each other. We know that the vertically opposite angles created when two lines intersect are equal. So $ \angle DEC=\angle BEF $ . The line BC cuts the parallel lines DC and AF and creates alternate angles $ \angle DCE $ and $ \angle FBE $ . We know that the alternate angles are equal. So $ \angle DCE=\angle FBE $ . \[\]
So we see in the triangle $ \Delta DEC $ and $ \Delta BEF $ that $ \angle CDE=\angle BFE,BE=CE,\angle DCE=\angle FBE $ . We use the Angle-Angle-Side congruence of triangles to conclude $ \Delta DEC\cong \Delta BEF $ . So the rest of the sides and angles will be equal. So $ CD=BF $ but from the parallelogram we have DC=AB. So we get BF=AB
Now the point B on the line segment is AF . So
\[\text{AF}=\text{ AB}+\text{BF}\]
Putting the values BF=AB in the above equation we get.
\[\text{AF}=\text{ AB}+\text{BF=AB+AB=2AB}\]
Which is the required proof.\[\]
Note: We need to be careful of the confusion between similarity and congruence. Similarity tells us about the ratios of angles and sides while congruence tells about equality of angles and sides. The question can also be framed with numerical value.
Complete step-by-step answer:

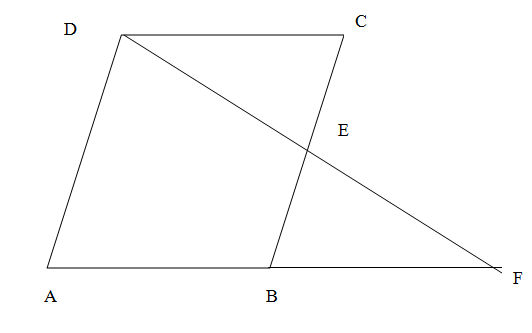
We see in the given figure that ABCD is a parallelogram which means the opposite sides are of equal length and opposite angles are of equal measurement. Mathematically,
\[AB=CD,AD=BC,\angle ADC=\angle ABC,\angle BAC=BCD\]
We are also given in the question that E is the midpoint of BC which means $ BE=CE $ . When DE and AB are extended they meet on a point F. We are asked to prove $ \text{AF}=\text{2AB} $ .\[\]
Let us observe the two triangles $ \Delta DEC $ and $ \Delta BEF $ . We see that the angles $ \angle DEC $ and $ \angle BEF $ are vertically opposite to each other. We know that the vertically opposite angles created when two lines intersect are equal. So $ \angle DEC=\angle BEF $ . The line BC cuts the parallel lines DC and AF and creates alternate angles $ \angle DCE $ and $ \angle FBE $ . We know that the alternate angles are equal. So $ \angle DCE=\angle FBE $ . \[\]
So we see in the triangle $ \Delta DEC $ and $ \Delta BEF $ that $ \angle CDE=\angle BFE,BE=CE,\angle DCE=\angle FBE $ . We use the Angle-Angle-Side congruence of triangles to conclude $ \Delta DEC\cong \Delta BEF $ . So the rest of the sides and angles will be equal. So $ CD=BF $ but from the parallelogram we have DC=AB. So we get BF=AB
Now the point B on the line segment is AF . So
\[\text{AF}=\text{ AB}+\text{BF}\]
Putting the values BF=AB in the above equation we get.
\[\text{AF}=\text{ AB}+\text{BF=AB+AB=2AB}\]
Which is the required proof.\[\]
Note: We need to be careful of the confusion between similarity and congruence. Similarity tells us about the ratios of angles and sides while congruence tells about equality of angles and sides. The question can also be framed with numerical value.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




