Question

There are 20 cylindrical pillars in a path. The radius of each pillar is $14\text{ cm}$ and height $1\text{ m}$. Find the cost of painting the curved surface of all pillars at the rate of $\text{Rs}\text{. 10 per}\text{.sq}\text{.m}$.

Answer 1

Hint: As given in the question the radius of each cylindrical pillar is $14\text{ cm}$ and height $1\text{ m}$. first, we calculate the curved surface area of one pillar by using the formula $2\pi rh$ and multiply the area with $20$ as there are $20$ cylindrical pillars in a path. Now, to find the cost of painting the curved surface of all pillars multiply the total curved surface area of $20$ pillars with a rate of $\text{Rs}\text{. 10 per}\text{.sq}\text{.m}$.

Complete step-by-step solution:
We have given that the number of cylindrical pillars in a path $=20$.
The radius of each pillar is $14\text{ cm}$ and height $1\text{ m}$.

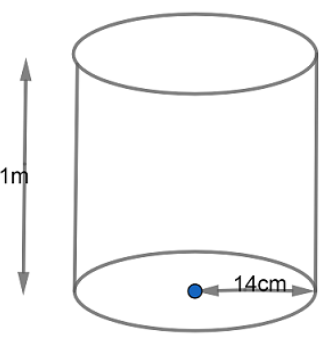
We have to find the cost of painting the curved surface of all pillars.
First, we have to convert the unit of radius from cm to m, we know that
So, the radius will be $14\text{ cm=}\dfrac{14}{100}m$
Now, we calculate the curved surface area of one pillar.
We know that the curved surface area of the cylinder is given by $2\pi rh$
Where, $r=$ radius and $h=$ height of cylinder
Now, substituting the values of radius and height and $\pi =\dfrac{22}{7}$, we get
Curved surface area $=2\times \dfrac{22}{7}\times \dfrac{14}{100}\times 1$
Curved surface area \[=\dfrac{2\times 22\times 2}{100}\]
Curved surface area \[=\dfrac{88}{100}=0.88\text{ }{{\text{m}}^{2}}\]
Now, the curved surface area of $20$ pillars will be $0.88\times 20=17.6\text{ }{{\text{m}}^{2}}$
Now, we have to calculate the cost of painting all $20$ pillars when the rate is $\text{Rs}\text{. 10 per}\text{.sq}\text{.m}$.
Now, we multiply the total surface area with the rate per sq. m., we get
$\begin{align}
  & 17.6\times 10 \\
 & =\text{ Rs}\text{. 176} \\
\end{align}$
So, the total cost of painting the curved surface of all pillars is $\text{Rs}\text{. 176}$.

Note: The mistake can be made during the conversion of units because it is necessary to have the same unit of all the dimensions. If we use the value with different units, we will get an incorrect answer. Also, one can use the total surface area of the cylinder instead of a curved surface area which leads to an incorrect solution. As both are different, the total surface area is used for 3D figures but in this question the curved surface of pillars is to be painted it means only side view, not top and bottom surfaces.