Question

There are 100 students in a class. In an examination, 50 of them failed in Mathematics, 45 failed in Physics, 40 failed in Biology and 32 failed in exactly two of the three subjects. Only one student passed in all the subjects. Then, the number of students failing in all the three subjects is?
A. 12
B. 4
C. 2
D. Cannot be determined from the given information

Answer 1

Hint: We have to write down the given information and by acknowledging it we will assume the variables and assign them to every possible outcome. With the help of Venn diagram, we form the equations and by using simple algebra we will solve them.

Complete Step-by-Step solution:
Given that there are 100 students and only one student passed in all 3 subjects.
So, the number of students failing in at least one subject are 99.
Let ‘a’ be the number of students failed only in Mathematics,
‘b’ be the number of students failed only in Physics and
‘c’ be the number of students who failed only in Biology.
Let ‘x’ be the number of students failed only in Mathematics and Physics,
‘y’ be the number of students failed only in Physics and Biology,
‘z’ be the number of students who failed only in Biology and Mathematics.
Let ‘p’ be the number of students who failed in all three subjects.
By using the concept of Venn diagram, we get

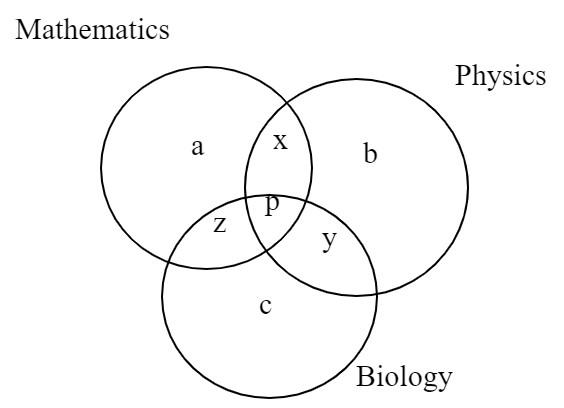
Number of students failed in at least one subject are 99 = a + b + c + x + y + z + p. … (1)
Number of students failed in exactly two subjects are 32 = x + y + z. … (2)
Students failed in Mathematics are 50 = a + x + p + z, … (3)
Students failed in Physics are 45 = b + x + y + p … (4) and
Students failed in Biology are 40 = c + y + z + p. … (5)
By adding equations (1), (2) and (3), we get
135 = a + b + c + 2(x + y + z) + 3p
By grouping the above equation:
$ \Rightarrow $ 135 = (a + b + c + x + y + z + p) + (x + y + z) +2p
Now, substitute the values in above equation by using equation (1) and (2)
$ \Rightarrow $ 135 = 99 + 32 + 2p
$ \Rightarrow $ 2p = 135 – 131
$ \Rightarrow $ p = $\dfrac{4}{2}$ = 2
Hence, p = 2 which refers to the number of students failed in all three subjects.
Therefore, option C. is correct.

Note: A Venn diagram is a diagram that shows all possible logical relations between a finite collection of different sets. Students must follow this approach as it is the easiest and most feasible way to solve these types of questions, other ways can be tedious and may lead us to wrong answers. Also will consume an enormous amount of time.