Question

The Young's modulus a rubber string 8 cm long and density $\text{1}\text{.5 kg / }{{\text{m}}^{\text{3}}}$ is $\text{5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{8}}}\text{ N/}{{\text{m}}^{\text{2}}}$, is suspended on the ceiling in a room. The increases in length due to its own weight will be:
(A). $\text{9}\text{.6 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-\text{5}}}\text{ m}$
(B). $\text{9}\text{.6 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-\text{11}}}\text{ m}$
(C). $\text{9}\text{.6 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-\text{3}}}\text{ m}$
(D). 9.6 m

Answer 1

Hint: Before we answer this question, we should be having knowledge about elasticity and the concept of Young’s modulus. Young’s modulus gives us a relationship between strain and stress in a material. So, it is important to begin the answer by defining Young’s modulus.

Complete Step-by-step solution:
Young’s modulus is defined as the mechanical property which measures the stiffness of a solid material. It develops a relationship between the stress and strain, occurring in a body, in the linear elasticity regime, in case of a uniaxial deformation.
Young’s modulus is defined as Y.

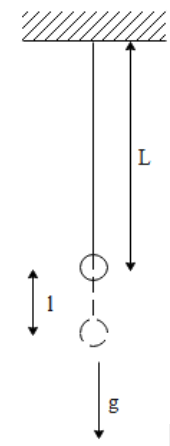
This diagram demonstrates the question.
Let us first see the values which are provided in the question. According to the question,
The length of the rubber band, or L.
The density is given as d which is $\text{1}\text{.5 kg / }{{\text{m}}^{\text{3}}}$.
Young’s modulus or as we know Y is given as $\text{5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{8}}}\text{ N/}{{\text{m}}^{\text{2}}}$.
So we have to find the relation between the increase in length and the Young’s modulus. The relationship is given as follows:
$\text{l =}\dfrac{{{\text{L}}^{\text{2}}}\text{dg}}{\text{2Y}}$
In the above formula the variables denote the following,
l represents the increase in length
g represents the acceleration due to gravity
So let us put the values which are presented in the question. We should remember that when the value of g is not given, we can consider it to be as 10.
Therefore, the expression is as follows:
$\text{l = }\dfrac{{{\text{(8 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-\text{2}}}\text{)}}^{\text{2}}}\text{ }\!\!\times\!\!\text{ 1}\text{.5 }\!\!\times\!\!\text{ 10}}{\text{2 }\!\!\times\!\!\text{ 5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{8}}}}\text{ = 9}\text{.6 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-\text{11}}}\text{m}$
Therefore, we can say that the increase in length is equal to $\text{9}\text{.6 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-\text{11}}}\text{ m}$ .
So, the correct answer is Option B.

Note: In the answer we have mentioned Young’s modulus as a relationship between stress and strain in a body. So it is required to know the meaning of these two concepts. By stress we mean the measure of force which is put on the object over the area. And by strain we mean change in length over the original length.