Question

The work done by a centripetal force in a circular motion:
A. increases by decreasing the radius of circle
B.decreases by increasing the radius of circle
C.increases by increasing the mass of the body
D.is always zero

Answer 1

Hint: Work done by a body is the dot product of force and displacement in the direction of force. It is zero if the force vector and displacement vector are perpendicular.
Centripetal force is responsible for circular motion performed by a body and it always acts towards the Centre.

Complete answer:
When a body is performing a circular motion a force acts on it which is responsible for its motion which is centripetal force .It is always acting towards the radius of the circular path in which the body is moving.
Work done by centripetal force =centripetal force$\overset{\to }{\mathop{\left( {{F}_{C}} \right)}}\,$ $\times $ displacement of the body $\left( \overset{\to }{\mathop{s}}\, \right)$
Work done by a force is non zero only when the force vector and displacement vector are not perpendicular which means angle between them should not be ${{90}^{o}}$.

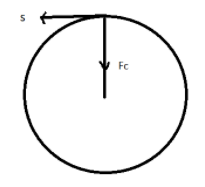
But as seen in the figure the displacement vector is perpendicular to the force vector which means work done by centripetal force on the body is zero throughout the motion of the body irrespective of whether we increase the mass of the body or radius of the body, or if we decrease the radius of the body.

So, the correct option of this question is D.

Note:
Centripetal force does not exist on its own but it is the net force acting on the body which provides necessary centripetal force to move on the circular path when many forces are acting on the body.
There are two types of circular motion
1.uniform circular motion
2.non-uniform circular motion.
Centrifugal force is equal in magnitude to the centripetal force but it acts away from the Centre of the circle