
The volume of the largest possible right circular cylinder that can be inscribed in a sphere of radius = $\sqrt 3 $ is:-
A. $\dfrac{4}{3}\sqrt 3 \pi $
B. $2\pi $
C. $\dfrac{8}{3}\sqrt 3 \pi $
D. $4\pi $
Answer
576.6k+ views
Hint: Here in this question two concepts will get which are mentioned below:-
1. Volume of a cylinder = $\pi {r^2}h$ (where ‘r’ is the radius of cylinder and ‘h’ is the height of the cylinder)
2. Condition for maxima:-A function f(x) has a local maxima or local maximum value at a point $x_0$ if the values of f(x) of f for ‘x’ near $x_0$ are all less than f($x_0$). We can find maxima of a function f on an interval [a,b] as follows:-
Complete step-by-step answer:
Draw a sphere of radius $\sqrt 3 $ having a cylinder inscribed in it having radius ‘r’ and height ‘h’.
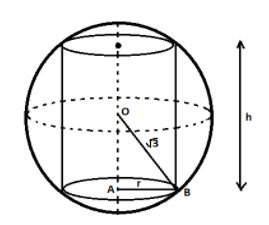
Now in triangle AOB, we will apply Pythagoras theorem as $\angle OAB = {90^ \circ }$
$ \Rightarrow O{A^2} + A{B^2} = O{B^2}$
Now we will put values of OA = half of the cylinder height, OB = radius of sphere given $\sqrt 3 $, AB = radius of a cylinder.
$ \Rightarrow {(\dfrac{h}{2})^2} + {r^2} = {(\sqrt 3 )^2}$
$ \Rightarrow {\dfrac{h}{4}^2} + {r^2} = 3$
$ \Rightarrow {r^2} = 3 - {\dfrac{h}{4}^2}$ ......................... (Equation 1)
Now Volume of a cylinder = $\pi {r^2}h$ (where ‘r’ is the radius of cylinder and ‘h’ is the height of the cylinder)
$ \Rightarrow V = \pi (3 - {\dfrac{h}{4}^2})h$ (From equation 1)
$ \Rightarrow V = \pi (3h - {\dfrac{h}{4}^3})$ (Multiplying h inside) ....................... (Equation 2)
Now we will derive V in terms of ‘h’
$ \Rightarrow V' = \pi (3 - {\dfrac{{3h}}{4}^2})$
For maximum condition we will put \[V' = 0\]
$ \Rightarrow \pi (3 - {\dfrac{{3h}}{4}^2}) = 0$
$ \Rightarrow 3 = {\dfrac{{3h}}{4}^2}$
Now we will cancel 3 from both sides and then solve for value of ‘h’
$ \Rightarrow {h^2} = 4$
$ \Rightarrow h = \pm 2$
Now we will check condition of maxima by doing double derivative of the function with respect to ‘h’
$ \Rightarrow V'' = 0 - \dfrac{{6h}}{4}$
$ \Rightarrow V'' = - \dfrac{{6h}}{4}$
As $V'' < 0$ this is the condition for local maxima, therefore maximum value will be obtained by putting $h = 2$ in equation 1
$ \Rightarrow V = \pi (3 - {\dfrac{2}{4}^2})2$
$ \Rightarrow V = \pi (3 - 1)2$
$ \Rightarrow V = 4\pi $
So, the correct answer is “Option D”.
Note: Students may likely to make mistake while determining whether it is a case of maxima or minima so here below brief explanation is mentioned:-
Condition of maxima is mentioned in hints.
Condition for minima:-A function f(x) has local minima at a point $x_0$ if the values of f(x) of f for ‘x’ near $x_0$ are all greater than f($x_0$). We can find minima of a function f on an interval [a,b] as follows:-
*Solve $f'(x) = 0$ to find critical points of ‘f’
*Now double derivative the function and check if it is greater than zero then there will be
minimum value at that critical point.
1. Volume of a cylinder = $\pi {r^2}h$ (where ‘r’ is the radius of cylinder and ‘h’ is the height of the cylinder)
2. Condition for maxima:-A function f(x) has a local maxima or local maximum value at a point $x_0$ if the values of f(x) of f for ‘x’ near $x_0$ are all less than f($x_0$). We can find maxima of a function f on an interval [a,b] as follows:-
*Solve $f'(x) = 0$ to find critical points of ‘f’
*Now double derivative the function and check if it is less than zero then there will
be maximum value at that critical point.
Complete step-by-step answer:
Draw a sphere of radius $\sqrt 3 $ having a cylinder inscribed in it having radius ‘r’ and height ‘h’.

Now in triangle AOB, we will apply Pythagoras theorem as $\angle OAB = {90^ \circ }$
$ \Rightarrow O{A^2} + A{B^2} = O{B^2}$
Now we will put values of OA = half of the cylinder height, OB = radius of sphere given $\sqrt 3 $, AB = radius of a cylinder.
$ \Rightarrow {(\dfrac{h}{2})^2} + {r^2} = {(\sqrt 3 )^2}$
$ \Rightarrow {\dfrac{h}{4}^2} + {r^2} = 3$
$ \Rightarrow {r^2} = 3 - {\dfrac{h}{4}^2}$ ......................... (Equation 1)
Now Volume of a cylinder = $\pi {r^2}h$ (where ‘r’ is the radius of cylinder and ‘h’ is the height of the cylinder)
$ \Rightarrow V = \pi (3 - {\dfrac{h}{4}^2})h$ (From equation 1)
$ \Rightarrow V = \pi (3h - {\dfrac{h}{4}^3})$ (Multiplying h inside) ....................... (Equation 2)
Now we will derive V in terms of ‘h’
$ \Rightarrow V' = \pi (3 - {\dfrac{{3h}}{4}^2})$
For maximum condition we will put \[V' = 0\]
$ \Rightarrow \pi (3 - {\dfrac{{3h}}{4}^2}) = 0$
$ \Rightarrow 3 = {\dfrac{{3h}}{4}^2}$
Now we will cancel 3 from both sides and then solve for value of ‘h’
$ \Rightarrow {h^2} = 4$
$ \Rightarrow h = \pm 2$
Now we will check condition of maxima by doing double derivative of the function with respect to ‘h’
$ \Rightarrow V'' = 0 - \dfrac{{6h}}{4}$
$ \Rightarrow V'' = - \dfrac{{6h}}{4}$
As $V'' < 0$ this is the condition for local maxima, therefore maximum value will be obtained by putting $h = 2$ in equation 1
$ \Rightarrow V = \pi (3 - {\dfrac{2}{4}^2})2$
$ \Rightarrow V = \pi (3 - 1)2$
$ \Rightarrow V = 4\pi $
So, the correct answer is “Option D”.
Note: Students may likely to make mistake while determining whether it is a case of maxima or minima so here below brief explanation is mentioned:-
Condition of maxima is mentioned in hints.
Condition for minima:-A function f(x) has local minima at a point $x_0$ if the values of f(x) of f for ‘x’ near $x_0$ are all greater than f($x_0$). We can find minima of a function f on an interval [a,b] as follows:-
*Solve $f'(x) = 0$ to find critical points of ‘f’
*Now double derivative the function and check if it is greater than zero then there will be
minimum value at that critical point.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




