Question

The volume of right circular cylinder, whose diameter is 10cm and height 4cm is
A. $40\pi c{m^3}$
B. $20\pi c{m^3}$
C. $100\pi c{m^3}$
D. $80\pi c{m^3}$

Answer 1

Hint: Before attempting this question, one must have prior knowledge about the right circular cylinder and also remember that volume of the right circular cylinder is given as; volume of cylinder = $\pi {r^2}h$, using this information will help you to approach the solution of the problem.

Complete step by step answer:

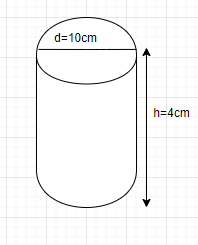
Given that the height of cylinder = 4cm
And diameter of cylinder = 10cm
Now, we have to find the volume of the cylinder.
Let us first calculate the radius of cylinder, i.e.
$r = \dfrac{d}{2}$ here d is the diameter of the given right circular cylinder
$ = \dfrac{{10}}{2}$
Or r = 5cm
Now, we know that the volume of cylinder =$\pi {r^2}h$
Putting the values of $\pi ,r,h$ in above formula we get,
Volume of right circular cylinder$ = \dfrac{{22}}{7} \times {\left( 5 \right)^2} \times 4$
Or volume of cylinder$ = \dfrac{{22}}{7} \times 25 \times 4$
As we can see that the options are in $\pi $ form thus we do not eliminate $\pi $
Now, volume of cylinder $ = 100\pi c{m^3}$

So, the correct answer is “Option C”.

Note: In the above solution we came across the term “right circular shape” which can be described as the three-dimensional shape which consist of circular base and whose elements are perpendicular to the base and the axis of the right circular cylinder is formed by joining the line to the center of the circular bases there are some properties shown by the cylinder such as the bases of the cylinder are always parallel and congruent to each other, when the bases of the cylinder is in form of ellipse it is named as the elliptical cylinder, axis of right circular cylinder form right angle with base.