Question

The volume of a right circular cone is 4710 cu.cm. if the radius and height of the cone are in the ratio $ 3:4 $ , find its slant height, when $ \pi =3.14 $ . \[\]

Answer 1

Hint: We take the length of the radius as $ r=3x $ cm, then length of height will be $ h=4x $ cm. We use formula for volume of cone $ \dfrac{1}{3}\pi {{r}^{2}}h $ in terms of $ x $ and equate it to given volume 4710. We solve for $ x $ and the find the slant height as $ l=\sqrt{{{h}^{2}}+{{r}^{2}}} $ .\[\]

Complete step by step answer:
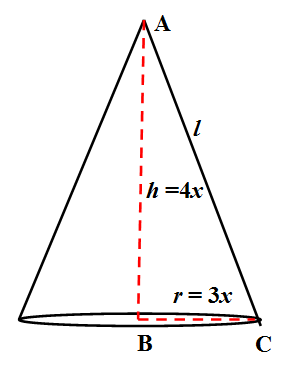
We have drawn the figure of the right circular cone above with apex A and the center of circular base B and C a point on the circular base. The line segment joining the apex to the center is the height of the conies called height and denoted as $ h $ and the line segment joining the apex to any point the circular base is called slant height and denoted as $ l $. We use Pythagoras theorem in triangle ABC and find the length of slant height as
\[l=\sqrt{{{h}^{2}}+{{r}^{2}}}\]

We are given in the question that the radius and height of the cone are in the ratio $ 3:4 $. Let us assume for the length of the radius as $ r=3x $ cm then by the law of ratio length of height will be $ h=4x $ cm. We know that the volume of a right circular cone with radius $ r $ and height $ h $ is given by $ V=\dfrac{1}{3}\pi {{r}^{2}}h $ but we are given that the volume of the cone is 4710 cubic centimeter.
\[\begin{align}
  & V=\dfrac{1}{3}\pi {{r}^{2}}h \\
 & \Rightarrow 4710=\dfrac{1}{3}\times 3.14\times {{\left( 3x \right)}^{2}}\times 4x \\
 & \Rightarrow 4710\times 3=3.14\times 36{{x}^{3}} \\
 & \Rightarrow {{x}^{3}}=\dfrac{4710\times 3}{3.14\times 36} \\
 & \Rightarrow {{x}^{3}}=125 \\
\end{align}\]
We take cube root both side to have;
\[x=5\text{ cm}\]
So the length of the radius is $ r=3x=3\times 5=15 $ cm and length of the height is $ h=4x=4\times 5=20 $ cm. So the slant height of the cone is
\[l=\sqrt{{{h}^{2}}+{{r}^{2}}}=\sqrt{{{15}^{2}}+{{20}^{2}}}=25\text{ cm}\]

Note:
We note from the law of ratio that we multiply a non-zero number $ k $ to the ratio $ a:b $, the value will not change which means $ ka:kb=a:b $. We can prime factorize 4710 for quicker calculation. We can find the curved surface area of the cone using the formula $ {{A}_{c}}=\pi rl $ and total surface area using the formula $ A=\pi rl+\pi {{r}^{2}} $ .