Question

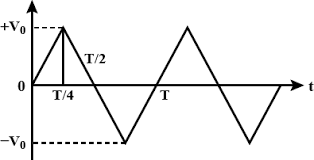
The voltage time (V-t) graph for triangular waves having peak value ${V}_{0}$ is as shown in figure. The rms value of V in time interval from t=0 to $\dfrac { T }{ 4 }$ is:

A. $\dfrac { { V }_{ 0 } }{ \sqrt { 3 } }$
B. $\dfrac { { V }_{ 0 } }{ 2 }$
C. $\dfrac { { V }_{ 0 } }{ \sqrt { 2 } }$
D. None of these

Answer 1

Hint: We have to calculate rms value of voltage. As the name itself explains, rms voltage is calculated by taking the square root of the mean average of the square of the voltage in an appropriately chosen time interval which is already mentioned in the question. Substitute the values in the rms formula and calculate the rms value of V in a time interval from t=0 to $\dfrac { T }{ 4 }$.

Complete step by step answer:
Given: Peak value of the triangular wave is ${V}_{0}$
For t=0 to $\dfrac { T }{ 4 }$,
$\dfrac { V }{ t } =\dfrac { { V }_{ 0 }-0 }{ \dfrac { T }{ 4 } -0 }$
$\Rightarrow \dfrac { V }{ t } =\dfrac { { V }_{ 0 } }{ \dfrac { T }{ 4 } }$
$\Rightarrow V=\dfrac { 4{ { V }_{ 0 } } }{ { T }_{ 0 } } t$
RMS value is given by,
${ V }_{ rms }=\sqrt { \dfrac { \int _{ 0 }^{ T }{ { V }^{ 2 }dt } }{ T } }$
Substituting the values in above equation we get,
${ V }_{ rms }=\sqrt { \dfrac { \int _{ 0 }^{ \dfrac { T }{ 4 } }{ { \left( \dfrac { 4{ V }_{ 0 } }{ T } t \right) }^{ 2 }dt } }{ \dfrac { T }{ 4 } } }$
$\Rightarrow { V }_{ rms }=\sqrt { \dfrac { \dfrac { 16{ V }_{ 0 }^{ 2 } }{ { T }^{ 2 } } \int _{ 0 }^{ \dfrac { T }{ 4 } }{ { t }^{ 2 }dt } }{ \dfrac { T }{ 4 } } }$
$\Rightarrow { V }_{ rms }=\sqrt { \dfrac { 64{ V }_{ 0 }^{ 2 } }{ { T }^{ 3 } } \int _{ 0 }^{ \dfrac { T }{ 4 } }{ { t }^{ 2 }dt } }$
$\Rightarrow { V }_{ rms }=\sqrt { \dfrac { 64{ V }_{ 0 }^{ 2 } }{ { T }^{ 3 } } \int _{ 0 }^{ \dfrac { T }{ 4 } }{ \cfrac { { t }^{ 3 } }{ 3 } } }$
${ \Rightarrow V }_{ rms }=\sqrt { \dfrac { 64{ V }_{ 0 }^{ 2 } }{ { T }^{ 3 } } \times \dfrac { 1 }{ 3 } \left( \dfrac { { T }^{ 3 } }{ 64 } \right) }$
${ \Rightarrow V }_{ rms }=\sqrt { \dfrac { { V }_{ 0 }^{ 2 } }{ 3 } }$
${ \therefore V }_{ rms }=\dfrac { { V }_{ 0 } }{ \sqrt {3} }$
Thus, the rms value of V in time interval from t=0 to $\dfrac { T }{ 4 }$ is $\dfrac { { V }_{ 0 } }{ \sqrt { 3 } }$
Hence, the correct answer is option A i.e. $\dfrac { { V }_{ 0 } }{ \sqrt { 3 } }.$

Note:
RMS value of a half wave rectifier wave is the least as compared to other waveforms with the same peak value. RMS value for triangular, saw-tooth and sinusoidal waveforms is greater as compared to half-wave rectifiers but lesser than that of the square wave. Square wave has the highest RMS value as compared to all the other waveforms.