Question

The vertices of a triangle are $ A\left( 3,4 \right),B\left( 7,2 \right)\text{ and }C\left( -2,-5 \right) $ . Find the length of the median through the vertex A.
 $ \begin{align}
  & \text{A}\text{. }\dfrac{\sqrt{111}}{2}\text{ units} \\
 & \text{B}\text{. }\dfrac{\sqrt{147}}{2}\text{ units} \\
 & \text{C}\text{. }\dfrac{\sqrt{137}}{2}\text{ units} \\
 & \text{D}\text{. }\dfrac{\sqrt{122}}{2}\text{ units} \\
\end{align} $

Answer 1

Hint: To solve this question first we will draw a triangle $ \Delta ABC $ and a median $ AD $ through the vertex A. Then we will use the midpoint formula to find the coordinates of point D and then use the distance formula to find the length of the median AD.
The midpoint formula is given as $ x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2},y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2} $
The distance formula is given as $ \sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} $

Complete step by step answer:
We have been given the vertices of a triangle are $ A\left( 3,4 \right),B\left( 7,2 \right)\text{ and }C\left( -2,-5 \right) $ .
We have to find the length of the median through vertex A.
Let us draw a triangle $ \Delta ABC $ and a median $ AD $ through the vertex A.

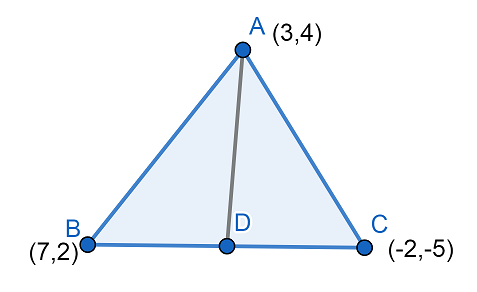
Now, we have to find the length of AD.
Now, we know that the median is a line segment joining the vertex to the mid-point of the opposite side thus bisects the side.
So, we get that AD bisects side BC at point D. So, to find the coordinates of point D we can use the midpoint formula.
Let us assume that the coordinates of point D be $ D(x,y) $ so the midpoint formula is given as $ x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2},y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2} $
So, the coordinates of D will be
 $ \begin{align}
  & \Rightarrow D(x,y)=\dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \\
 & \Rightarrow D(x,y)=\dfrac{7+\left( -2 \right)}{2},\dfrac{2+\left( -5 \right)}{2} \\
 & \Rightarrow D(x,y)=\dfrac{7-2}{2},\dfrac{2-5}{2} \\
 & \Rightarrow D(x,y)=\dfrac{5}{2},\dfrac{-3}{2} \\
\end{align} $
Now, we know that the length of AD is equal to the distance between points A and D. Now, the distance formula will be used to calculate the length of AD.
 $ \Rightarrow \sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}} $
Now, we have $ \left( {{x}_{1}},{{y}_{1}} \right)=\left( 3,4 \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)=\left( \dfrac{5}{2},\dfrac{-3}{2} \right) $
Substituting the values and solving further we get
\[\begin{align}
  & \Rightarrow \sqrt{{{\left( \dfrac{5}{2}-3 \right)}^{2}}+{{\left( \dfrac{-3}{2}-4 \right)}^{2}}} \\
 & \Rightarrow \sqrt{{{\left( \dfrac{5-6}{2} \right)}^{2}}+{{\left( \dfrac{-3-8}{2} \right)}^{2}}} \\
 & \Rightarrow \sqrt{{{\left( \dfrac{-1}{2} \right)}^{2}}+{{\left( \dfrac{-11}{2} \right)}^{2}}} \\
 & \Rightarrow \sqrt{\dfrac{1}{4}+\dfrac{121}{4}} \\
 & \Rightarrow \sqrt{\dfrac{\left( 1+121 \right)}{4}} \\
 & \Rightarrow \dfrac{\sqrt{122}}{2} \\
\end{align}\]
So, the length of the median through the vertex A is $ \dfrac{\sqrt{122}}{2}\text{ units} $ .

Option D is the correct answer.

Note:
Students must be careful while drawing the diagram. Draw a median through vertex A only because the scalene triangle length of all medians are different. Also, avoid calculation mistakes because it leads to the wrong answer.