Question

The vertices of a parallelogram are (3, – 2), (4, 0), (6, – 3), and (5, – 5). The diagonal intersect at a point M. The coordinates of the point M are

Answer 1

Hint: We are given the vertex of the parallelogram. Firstly, we will understand how a diagonal and point of intersection of diagonal related to each other. Then we use the mid – point formula which is given as \[x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}\] and \[y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2},\] where (x, y) is coordinate of the midpoint while \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] are the coordinates of the corner points.

Complete step by step answer:
We are given that we have a parallelogram whose coordinates of the vertices are as (3, – 2), (4, 0), (6, – 3), and (5, – 5). We are mentioned that the diagonal of the parallelogram intersect each other at M, we are asked to find the coordinate of M. To find the coordinate of the point M, we must have the information of the parallelogram and its diagonal.
So, we have that parallelogram is a special type of quadrilateral in which the opposite is equal and parallel. The diagonal of the parallelogram are not equal in the length because at the vertex, the angle is not \[{{90}^{\circ }}.\]

In the above parallelogram ABCD, AC and BD are diagonal. We know that when the diagonal meet each other, they do not just intersect basically they bisect each other. So, the diagonals bisect each other. So, the point where the diagonal of the parallelogram intersect is nothing but the midpoint of the diagonal.

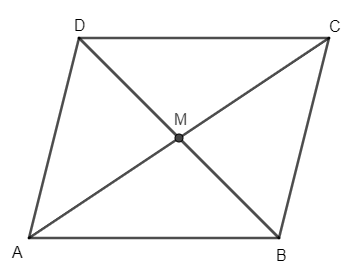
Here, M is the midpoint of AC and BD.
Now, let ABCD be our parallelogram with A(3, – 2), B(4, 0), C(6, – 3), and D(5, – 5).

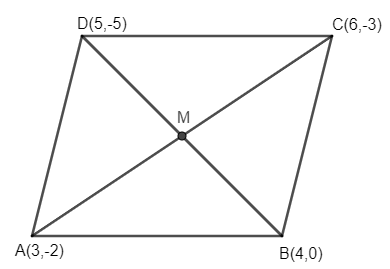
Now, we know that the point of intersection of the diagonal (M) is the midpoint of the diagonal. So, we apply midpoint formula on the diagonal AC, A(3, – 2) and C(6, – 3). The midpoint formula is as follows
\[x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}\]
\[y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}\]
So, consider \[\left( {{x}_{1}},{{y}_{1}} \right)=\left( 3,-2 \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)=\left( 6,-3 \right)\] and consider the point of M as M(x, y). So, using the above formula, we get,
\[\Rightarrow x=\dfrac{3+6}{2}\]
\[\Rightarrow x=\dfrac{9}{2}\]
And similarly,
\[\Rightarrow y=\dfrac{-2+\left( -3 \right)}{2}\]
On simplifying, we get,
\[\Rightarrow y=\dfrac{-2-3}{2}\]
\[\Rightarrow y=\dfrac{-5}{2}\]
So, we get, coordinate of M as \[M\left( x,y \right)=M\left( \dfrac{9}{2},\dfrac{-5}{2} \right).\]
Note:
Remember that we do not have to solve for both the diagonal, we can just find the midpoint of any one diagonal and we can choose AC or BD. Using any one of the two we can be easily to find the coordinate of M and to be sure about the answer one can recheck by finding the midpoint of the other diagonal.