Question

The vertex angle of an isosceles triangle measures $84^\circ $. What is the measure of base angle?
A.$40^\circ $
B.$42^\circ $
C.$46^\circ $
D.$48^\circ $

Answer 1

Hint: We know that the sum of all angles of a triangle is $180^\circ $. An isosceles triangle consists of two base angles and one vertex angle. We can say that the measure of two base angles will be the same. Add the vertex angle and base angles equate them to $180^\circ $, find the measure of base angle.

Complete step-by-step answer:
We know that an isosceles triangle consists of a vertex angle and two base angles. Length of two sides of the isosceles triangle is equal. So, the measure of two base angles of the isosceles triangle is equal.
Let us consider the measure of base angle to be $x$ degree. So, the measure of two angles are $x$ and $x$. The measure of vertex angle is $84^\circ $.
 

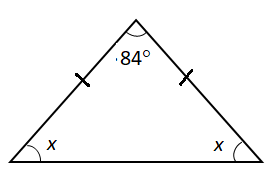
We know that the sum of all angles of a triangle is $180^\circ $. We can calculate the measure of base angle as:
\[x + x + 84^\circ = 180^\circ \]
\[ \Rightarrow 2x + 84^\circ = 180^\circ \]
 Subtract $84^\circ $ from both the sides of the above equation, we get
\[ \Rightarrow 2x = 96^\circ \]
 Divide both the sides by 2 to find the measure of base angle.
\[ \Rightarrow \dfrac{{2x}}{2} = \dfrac{{96^\circ }}{2}\]
\[ \Rightarrow x = 48^\circ \]
Therefore, the measure of the base angle of the isosceles triangle is $48^\circ $.
So, option (D) is the correct answer.

Note: We need to recognise that the measure of two base angles of an isosceles triangle is equal to each other as they are formed by two equal sides. Carefully consider that the missing two angles are base angles. So, consider the other two angles as $x$.
If we consider two equal angles of an isosceles triangle as $84^\circ $, then it may lead to incorrect answers.