Question

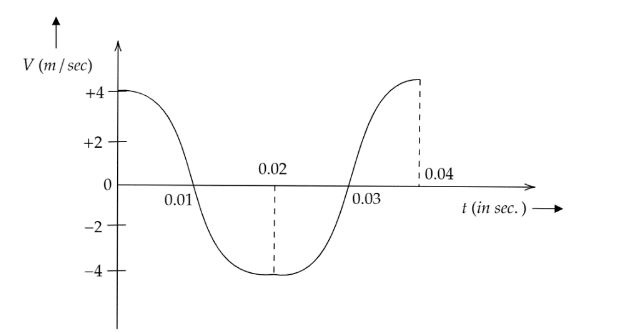
The velocity-time diagram of a harmonic oscillator is shown in the adjoining figure.The frequency of oscillation is:

A. $25{\text{ }}Hz$
B. $50{\text{ }}Hz$
C. $12.25{\text{ }}Hz$
D. ${\text{33}}{\text{.3 }}Hz$

Answer 1

Hint:The figure consists of a velocity graph which is in the Y-axis and time graph which is in the X-axis of the harmonic oscillator. We have to find the frequency of the oscillator which we will find from the total time period from the graph. The inverse of the total time period is the frequency.

Complete step by step answer:
The velocity of a particle is defined as the displacement it covers in that period of time.
The curve in the figure is a sinusoidal curve. It is not a continuous curve as it gets stopped at $0.04{\text{ }}\sec $. Hence, it confirms that the harmonic oscillator operates till $0.04{\text{ }}\sec $.So, the total time period of the harmonic oscillator is $0.04{\text{ }}\sec $.

The formula to find the frequency of a particle from total time period is given by,
$f = \dfrac{1}{T}$
Where, $f$ is the frequency of the harmonic oscillator and $T$ is the total time period till which the harmonic oscillator operates.
From the given graph we get the total time period $T = 0.04{\text{ }}\sec $
So, the frequency is,
$f = \dfrac{1}{T} \\
\Rightarrow f= \dfrac{1}{{0.04}} \\
\therefore f= 25\,Hz$
So, the frequency of the harmonic oscillator is $25{\text{ }}Hz$.

Therefore, the correct option is A.

Note:It must be noted that the frequency of a particle is defined as the number of waves that passes a fixed point in unit time or may be also considered as the number of cycles of vibration by a particle undergone in unit time. The SI unit of frequency is Hertz.