Question

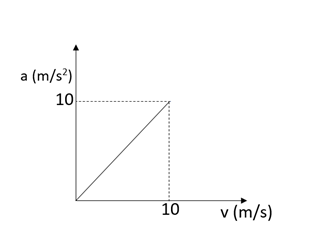
The velocity versus displacement graph of a particle which is moving in a straight line has been represented in the diagram. The corresponding acceleration versus velocity graph can be shown as,

A.

B.

C.

D.

Answer 1

Hint: The velocity axes will be equivalent to the displacement axis. As we all know that the first derivative of the velocity can be defined as the acceleration and the first derivative of the displacement with respect to the time taken can be described as the velocity. This will help you in answering this question.

Complete answer:
From the graph it will be clear that the velocity axes will be equivalent to the displacement axis. That is we can write that,
$v=s$
As we all know that the first derivative of the velocity can be defined as the acceleration and the first derivative of the displacement with respect to the time taken can be described as the velocity. This can be written as an equation given as,
$\dfrac{dv}{dt}=a$
And also we can write that,
$\dfrac{ds}{dt}=v$
As the velocity axis and the displacement axis are similar, we can differentiate both these equations with respect to the time taken which will be also equivalent. That is we can write that,
$\dfrac{dv}{dt}=\dfrac{ds}{dt}$
Putting the values we get, we can write that,
$a=v$
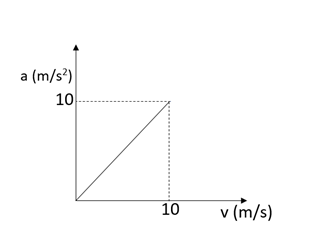
Therefore the acceleration velocity graph will be linear with a slope found to be one.

This has been mentioned as the option A.

Note:
The velocity can be defined as the variation of the displacement of the object with respect to the time taken. The displacement of the body can be defined as the perpendicular distance between the initial and the final positions of the body. Both these quantities are found to be vectors.