
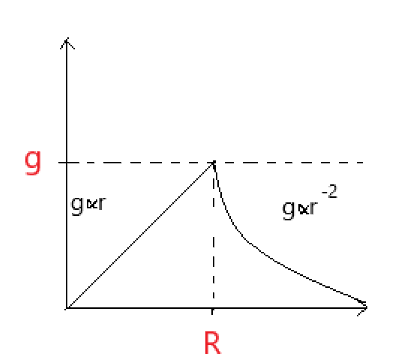
The variation of g with height or depth (r) is shown correctly by the graph in figure (where R is the radius of the earth).
A.
B.
C.
D.




Answer
598.2k+ views
Hint: For this question we start with the equation for g with respect to distance r from the center of the earth with mass M and radius R that is $g = \dfrac{{GM}}{{{r^2}}}$ . Then we find the expression of g when r< R that is ${g^1} = g\left( {1 - \dfrac{{2r}}{R}} \right)$ and when r>R that is ${g^1} = g{\left( {1 + \dfrac{r}{R}} \right)^{ - 2}}$ from these we get the relation of g with respect to r as $ \Rightarrow {g^1} \propto \left( {R - 2r} \right)$ and $ \Rightarrow {g^1} \propto \dfrac{1}{{{r^2}}}$ respectively.
Complete Step-by-Step solution:
We know that the acceleration due to gravity is denoted by the symbol g and is defined as the acceleration of an object because of the force acting on that object by the gravitational field of Earth. This force is written as
$F = mg$
Here m is the mass of the object. If $m = 1$, we get
$F = g$
This also says that g is the force on the unit mass. The g is independent of the mass of the body and can be accurately calculated in various ways.
Now we will try to see the variation of g with respect to height h. So let us assume an object of mass m, then the measure of the gravitational field strength $g$, at a distance r from the center of the earth with mass $M$ is given by:
$g = \dfrac{{GM}}{{{r^2}}}$
Now take the object at the surface of the earth that is r=R as shown in figure 1.
Here R is the radius of the earth. We get
$g = \dfrac{{GM}}{{{R^2}}}$-------------------------------- (1)
Now we assume that the object is at a height H from the surface of the earth as shown in figure 2.
${g^1} = \dfrac{{GM}}{{{{\left( {R + H} \right)}^2}}}$--------------------------- (2)
Now dividing equation (2) by (1) we get
${g^1} = \dfrac{{g{R^2}}}{{{{\left( {R + H} \right)}^2}}}$
$ \Rightarrow {g^1} = \dfrac{g}{{{{\left( {1 + \dfrac{H}{R}} \right)}^2}}}$
$ \Rightarrow {g^1} = g{\left( {1 + \dfrac{H}{R}} \right)^{ - 2}}$-------------------------(3)
This expression is used when $\dfrac{H}{R} \geqslant 1$ that is when the object is at a distance greater than the earth radius.
But when $\dfrac{H}{R} < 1$ we can Apply the binomial expansion and we will get
$ \Rightarrow {g^1} = g\left( {1 - \dfrac{{2H}}{R}} \right)$--------------------------- (4)
From these we can conclude that
Region 1: When $r \leqslant R$ we can write
$ \Rightarrow {g^1} = g\left( {1 - \dfrac{{2r}}{R}} \right)$
$ \Rightarrow {g^1} \propto \left( {R - 2r} \right)$
Region 2: When $r \geqslant R$ we can write
$ \Rightarrow {g^1} = g{\left( {1 + \dfrac{r}{R}} \right)^{ - 2}}$
$ \Rightarrow {g^1} \propto \dfrac{1}{{{r^2}}}$
So the graph we get is shown in figure 3
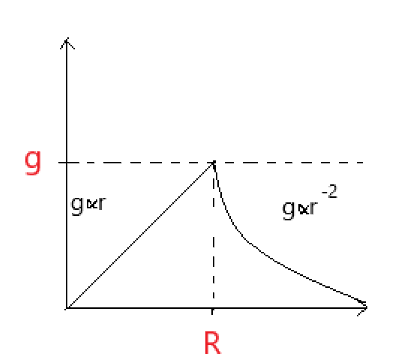
Figure 3
Hence option A is correct.
Note: We can also solve this question in a different way that is we get the expression of g with respect to r when $r < R$ as $g = \dfrac{{GM}}{{{R^3}}}r$ and when $r > R$ we get $g = \dfrac{{GM}}{{{r^2}}}$. By using these also we can plot the required graph.
Complete Step-by-Step solution:
We know that the acceleration due to gravity is denoted by the symbol g and is defined as the acceleration of an object because of the force acting on that object by the gravitational field of Earth. This force is written as
$F = mg$
Here m is the mass of the object. If $m = 1$, we get
$F = g$
This also says that g is the force on the unit mass. The g is independent of the mass of the body and can be accurately calculated in various ways.
Now we will try to see the variation of g with respect to height h. So let us assume an object of mass m, then the measure of the gravitational field strength $g$, at a distance r from the center of the earth with mass $M$ is given by:
$g = \dfrac{{GM}}{{{r^2}}}$
Now take the object at the surface of the earth that is r=R as shown in figure 1.

Figure 1
Here R is the radius of the earth. We get
$g = \dfrac{{GM}}{{{R^2}}}$-------------------------------- (1)
Now we assume that the object is at a height H from the surface of the earth as shown in figure 2.

Figure 2
${g^1} = \dfrac{{GM}}{{{{\left( {R + H} \right)}^2}}}$--------------------------- (2)
Now dividing equation (2) by (1) we get
${g^1} = \dfrac{{g{R^2}}}{{{{\left( {R + H} \right)}^2}}}$
$ \Rightarrow {g^1} = \dfrac{g}{{{{\left( {1 + \dfrac{H}{R}} \right)}^2}}}$
$ \Rightarrow {g^1} = g{\left( {1 + \dfrac{H}{R}} \right)^{ - 2}}$-------------------------(3)
This expression is used when $\dfrac{H}{R} \geqslant 1$ that is when the object is at a distance greater than the earth radius.
But when $\dfrac{H}{R} < 1$ we can Apply the binomial expansion and we will get
$ \Rightarrow {g^1} = g\left( {1 - \dfrac{{2H}}{R}} \right)$--------------------------- (4)
From these we can conclude that
Region 1: When $r \leqslant R$ we can write
$ \Rightarrow {g^1} = g\left( {1 - \dfrac{{2r}}{R}} \right)$
$ \Rightarrow {g^1} \propto \left( {R - 2r} \right)$
Region 2: When $r \geqslant R$ we can write
$ \Rightarrow {g^1} = g{\left( {1 + \dfrac{r}{R}} \right)^{ - 2}}$
$ \Rightarrow {g^1} \propto \dfrac{1}{{{r^2}}}$
So the graph we get is shown in figure 3

Figure 3
Hence option A is correct.
Note: We can also solve this question in a different way that is we get the expression of g with respect to r when $r < R$ as $g = \dfrac{{GM}}{{{R^3}}}r$ and when $r > R$ we get $g = \dfrac{{GM}}{{{r^2}}}$. By using these also we can plot the required graph.
Recently Updated Pages
Two men on either side of the cliff 90m height observe class 10 maths CBSE

Cutting of the Chinese melon means A The business and class 10 social science CBSE

Show an aquatic food chain using the following organisms class 10 biology CBSE

How is gypsum formed class 10 chemistry CBSE

If the line 3x + 4y 24 0 intersects the xaxis at t-class-10-maths-CBSE

Sugar present in DNA is A Heptose B Hexone C Tetrose class 10 biology CBSE

Trending doubts
The average rainfall in India is A 105cm B 90cm C 120cm class 10 biology CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

Who Won 36 Oscar Awards? Record Holder Revealed

Indias first jute mill was established in 1854 in A class 10 social science CBSE

Indias first jute mill was established in 1854 in A class 10 social science CBSE




