Question

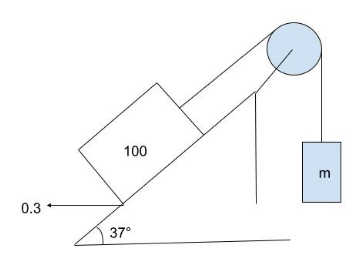
The value(s) of mass m for which the 100 kg block does not move upward?
A) 39 kg
B) 40 kg
C) 83 kg
D) 85 kg

Answer 1

Hint: Friction is an opposing force which opposes the relative motion or tendency or relative motion between two bodies. It is sometimes useful but sometimes has its own disadvantages.
There are different types of friction, in this question we will come across static friction and kinetic friction.
Static friction: It is present between the bodies who are stationary but have a tendency of relative motion. It is a variable and is self-adjusting depending upon the external force being applied. There is a limit beyond which the static friction will not act and the bodies will move and kinetic friction comes into light. That limit is called limiting friction.
Kinetic friction: When the applied force is greater than the limiting friction, then there is relative motion between them, kinetic friction is the opposing force. It is a constant and does not vary depending upon the applied force.
 $ {F_{\text{limiting}}} = {\mu _s}N $
 $ {F_k} = {\mu _k}N $
Where, N is normal force and $ {\mu _s},{\mu _k} $ are coefficients of static friction and kinetic friction respectively.

Complete Step By Step Answer:
Using the formula of static friction and kinetic friction, we will try to solve the question. There are two cases, when there is relative motion – kinetic friction and when there is no relative motion – static friction.
CASE 1: When the 100 kg block is pulling the hanging block up.
First, let’s draw a diagram with all the forces acting except frictional force.
Consider $ 100 = M $

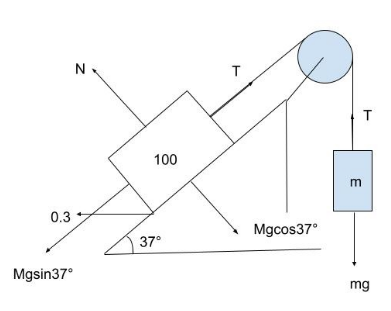
T is the tension and it is equal all through the rope. And g is gravity.
Here, the block is about to move. Hence the frictional force that’s going to act is kinetic friction.
The formula of kinetic friction is: $ {F_k} = {\mu _k}N $
The N is the normal force which is equal to $ 100(g\cos 37^\circ ) $
We know that $ g = 9.8\dfrac{m}{{{{\sec }^2}}} $ and $ \cos 37^\circ = \dfrac{4}{5} $
After further simplification, we get: $ 100(g\cos 37^\circ ) = 100 \times 9.8 \times \dfrac{4}{5} = 784Newtons $
Since, there is relative motion, the frictional force is pointed towards the rope. Against gravity.

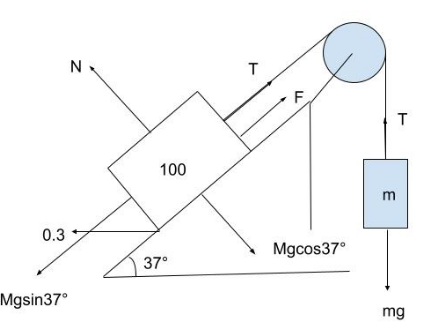
Writing an equation balancing all the forces, we get:
 $ 100(g\sin 37^\circ ) = T + F $
Substituting the value of F, we get:
 $ 100(9.8 \times \sin 37^\circ ) = T + [9.8 \times 0.3 \times (100 \times \cos 37^\circ )] $
 $ 588 = T + 235.2 $
On further simplification, we get:
 $ 588 - 235.2 = 352.8Newtons $
Since, the hanging mass is also not moving, writing a balance equation we get: $ T = mg $
Substituting, the value of T we get: $ 352.8 = 9.8m $
 $ m = 36kg $
This gives the minimum weight of the hanging block.
CASE 2: When the hanging block is pulling the 100 kg block up.
Here, the block is about to move. Hence the frictional force that’s going to act is kinetic friction.
The formula of kinetic friction is: $ {F_k} = {\mu _k}N $
First, let’s draw a diagram with all the forces acting except frictional force.
Consider $ 100 = M $

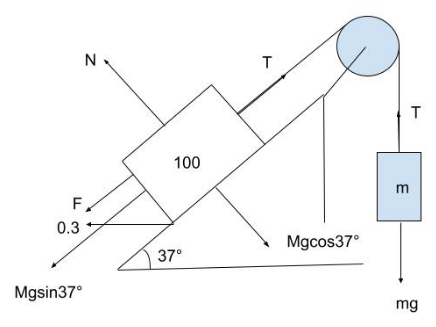
T is the tension and it is equal all through the rope. And g is gravity.
 $ {F_k} = {\mu _k}N $ .
We know that normal force acting on the 100 kg block will be: $ 100(g\cos 37^\circ ) $
We know that $ g = 9.8\dfrac{m}{{{{\sec }^2}}} $ and $ \cos 37^\circ = \dfrac{4}{5} $
After further simplification, we get: $ 100(g\cos 37^\circ ) = 100 \times 9.8 \times \dfrac{4}{5} = 784Newtons $
Writing the balance equations for both the 100 kg block we get:
 $ 100(g\sin 37^\circ ) + F = T $
After substituting the values of friction in the above equation, we get:
 $ 100(9.8 \times \sin 37^\circ ) + [9.8 \times 0.3 \times (100 \times \cos 37^\circ )] = T $
\[588 + 235.2 = T = 823.2\]
Now writing the balance equation for the hanging block, we get:
 $ T = mg $
Now substituting the value of tension, we get:
 $ 823.2 = 9.8m $
After further simplification, we get: $ m = 84kg $
This is the maximum weight of the block.
From the above two cases, we can say that:
If $ m \leqslant 36kg $ , then the hanging block of mass m will move upward and the block on the inclined plane will move downward.
If $ m \geqslant 84kg $ , then the hanging block of mass m will move downward and the block on the inclined plane will move upward.
Therefore, the right options are Option A, B, C.

Note:
When solving such questions, we need to draw free body diagrams of both the blocks and try balancing the forces on both the sides. When in the question they only mention $ \mu = 0.3 $ , this means that the coefficients of both static friction and kinetic friction is the same. One should avoid calculation mistakes while solving. A simple calculation mistake will give a wrong answer.