Question

The value of $\tan \left( {90 - \theta } \right)$ in the graph gives:

(A) Young’s modulus of elasticity
(B) Compressibility
(C) Shear strain
(D) Tensile strength

Answer 1

Hint: A stress-strain curve is a graphical representation of the reaction of a material when a load is applied. It is a comparison between stress and strain. These curves explain many of the properties of a material such as yield strength, ultimate tensile strength, and Young’s modulus.

Complete step by step solution:
Sine, Cosine, and Tangent are the three primary ratios in the trigonometry, based on which the whole trigonometric functions and formulas are designed. Each of the trigonometric functions has its equivalent importance. Actually, these ratios are used to find the sides and the angles of a right-angled triangle. So, these angles are calculated with respect to $\sin $, $\cos $ and $\tan $ functions.
(1) The trigonometry ratio of $\left( {{{90}^ \circ } - \theta } \right)$ will fall in the first quadrant.
(2) When we have the ${90^ \circ }$, then $\tan $ will become $\cot $.
(3) The sign of $\tan $ is positive in the first quadrant.
By considering the above points, we have,
$\tan \left( {{{90}^ \circ } - \theta } \right) = \cot \theta $
In a right-angled triangle, the cotangent of an angel is the ratio of length of the adjacent side to the length of the opposite side.
$\cot \theta = \dfrac{{adjacent\,side}}{{opposite\,side}}$

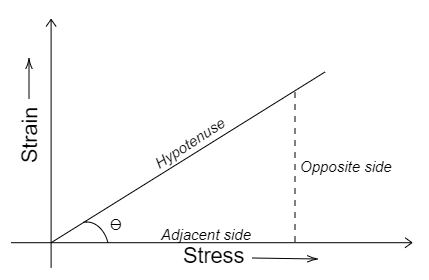
When the stress-strain curve forms the right-angled triangle and the stress-strain curve is assumed to be in the first quadrant.
 Then, $\tan \left( {{{90}^ \circ } - \theta } \right) = \cot \theta $
$\cot \theta = \dfrac{{stress}}{{strain}}$
$\text{Young’s modulus of elasticity }= \dfrac{\text{stress}}{\text{strain}}$

Young’s modulus of elasticity:
The Young’s modulus of elasticity is meaningful only in the range where the stress is proportional to the strain, and when the force is removed the material returns to its original dimensions. When the stresses increase, due to which the material may flow, undergoing permanent deformation, or finally break. Young’s modulus of elasticity is the ratio of longitudinal stress to longitudinal strain.
It is dented by $\dfrac{E}{Y}$.
Young’s modulus of elasticity is given by,
$E = \dfrac{\sigma }{\varepsilon }$
Where,
$E$ is Young’s modulus of elasticity
$\sigma $ is the uniaxial stress of the body
$\varepsilon $ is the strain or proportional deformation.

$\therefore$ The value of $\tan \left( {{{90}^ \circ } - \theta } \right)$ in the graph gives the Young’s modulus of elasticity. Hence, option (A) is correct.

Note:
The Young's Modulus is very important to scientists and doctors as this constant can insist them when a structural implant will get deform. And it will also help them to know how to design a piece mechanically for use in a body. SI unit of young’s modulus is Pascal $\left( {Pa} \right)$. $\left( {Pa = kg.{m^{ - 1}}.{s^{ - 2}}} \right)$.