Question

The value of g (acceleration due to gravity) at earth’s surface is 10$m{{s}^{-1}}$. It’s value at the centre of the earth which is assumed to be a sphere of radius R metre and uniform mass density is,
A. 5
$\text{B}\text{.}\dfrac{10}{R}$
$\text{C}\text{.}\dfrac{10}{2R}$
D. zero

Answer 1

Hint: Acceleration due to gravity is the acceleration of a body due to the force of gravity acting on it. Consider a point mass at a distance of r from the centre and at a depth of d from the surface. Then use the formula of gravitational force between two bodies is given as $F=G\dfrac{{{M}_{1}}{{M}_{2}}}{{{r}^{2}}}$. Then equate thus this to F=mg and find an expression for g.

Formula used:
$F=G\dfrac{{{M}_{1}}{{M}_{2}}}{{{r}^{2}}}$
F = ma

Complete step by step answer:
Any two bodies in the universe exert a force of attraction on each other. This force of attraction is called the gravitational force. The two forces are equal in magnitude but opposite in direction. The direction of the force exerted by body1 on body2 is always directed towards body1 and vice versa.
The magnitude of gravitational force depends on the two masses of the given bodies and the distance between the bodies. It is directly proportional to the product of masses (${{M}_{1}}$ and ${{M}_{2}}$) of the two bodies and inversely proportional to the square of the distance (r) between the centres of the bodies.
Therefore, the magnitude of gravitational force is given as $F=G\dfrac{{{M}_{1}}{{M}_{2}}}{{{r}^{2}}}$.
Hence, the bodies on earth are attracted towards it with a force of $F=G\dfrac{mM}{{{r}^{2}}}$ …….(i) where m is the mass of the body, M is the mass of earth and r is the distance of the body from the centre of earth.
According to Newton’s second law of motion F=ma, where m is the mass of the body and a is the acceleration of the body.
When it comes to gravity, the acceleration of the given body is called acceleration due to gravity and is denoted by g. Therefore, the force exerted on a body of mass m is F=mg ……(ii)
Let us now calculate the acceleration due to gravity of a body of mass m, inside earth at a depth of d from earth’s surface.
For this, we have to make certain assumptions. Assume that the given body is point sized. Let the shape of earth be a sphere of radius R and its mass density (mass distribution in the volume) be uniform everywhere.
Draw a figure of a sphere of radius R. Let the body be located at a distance of r from the sphere or depth d from the surface.
Draw an imaginary sphere with the same centre and radius r.

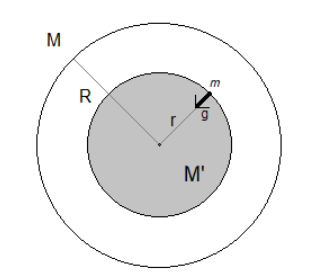
From here, consider the shaded sphere and non-shaded part of the whole sphere separately.
Let first calculate the force due the shaded sphere. Let the mass of this shaded sphere be M’. The force on the body due to this sphere will be $F=G\dfrac{mM'}{{{r}^{2}}}$.
Now, to calculate the force due to the non-shaded portion of the sphere, consider this portion as a shell of thickness d.
According to shell theory, the net force on a body inside a shell is zero.
Therefore, the force due to the non-shaded portion of the sphere will be zero.
Therefore, the net force exerted on the given body due to the complete sphere is $F=G\dfrac{mM'}{{{r}^{2}}}$, which is equal to mg.
Hence, $G\dfrac{mM'}{{{r}^{2}}}=mg$. Divide both sides of the equation by m.
$\Rightarrow g=G\dfrac{M'}{{{r}^{2}}}$ ……(iii).
However, we do not know the value of M’. Here we can use the uniform mass density. The mass density of the shaded sphere is equal to mass density of the bigger sphere.
i.e. $\dfrac{M'}{\dfrac{4}{3}\pi {{r}^{3}}}=\dfrac{M}{\dfrac{4}{3}\pi {{R}^{3}}}$ .
This implies, $M'=\dfrac{M{{r}^{3}}}{{{R}^{3}}}$.
Substitute this value of M’ in equation (iii).
We get, $\Rightarrow g=G\dfrac{\dfrac{M{{r}^{3}}}{{{R}^{3}}}}{{{r}^{2}}}$.
$\Rightarrow g=G\dfrac{Mr}{{{R}^{3}}}$ ……..(iv)
We know that r=R-d. Substitute of r in equation (iv).
We get, $\Rightarrow g=G\dfrac{M(R-d)}{{{R}^{3}}}$.
Therefore the expression of acceleration due to gravity of a body at a depth d from the surface of earth is $G\dfrac{M(R-d)}{{{R}^{3}}}$.
Here, we can understand that the acceleration of a body due to gravity inside earth decreases as we go from the surface to the centre of earth. At centre g=0.
Hence, the correct option is D.

Note: Although we found the expression for acceleration due to gravity of a point sized body, this is true only in ideal conditions. Remember we derived the expression for g by making several assumptions.
We assumed that the shape of earth is a sphere but it is not. We assumed that the mass density of earth is uniform everywhere but it is not. Mass density of earth varies from place to place. In addition, we assumed that the given body is a point size.
Therefore, in real cases the value of g will differ from the theoretical value.