Question

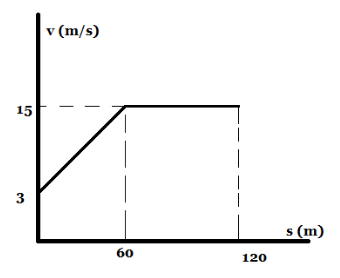
The $ v - s $ graph describing the motion of a motorcycle is shown in the figure. The time needed for the motorcycle to reach the position $ s = 120\;m $ [Given that $ \ln \;5 = 1.6 $ ] is $ 2\;x\;\sec $ , find $ x $ ?

Answer 1

Hint: Here we find the relation between the velocity $ v $ and the displacement $ s $ for the two curves separately. For the first half of the journey till $ s = 60\;m $ we will formulate the equation of the curve as $ v = \dfrac{s}{5} + 3 $ . For the second half of the journey from $ s = 60\;m $ to $ s = 120{\mkern 1mu} m $ , we see that $ v = 15\;m/s $ . In both these equations, we will substitute $ v = \dfrac{{ds}}{{dt}} $ and solve the integrations with appropriate limits.

Formula used:
 $ v = \dfrac{{ds}}{{dt}} $

Complete Step by step solution:
From the graph, we form the relationship between the velocity $ v $ and the displacement $ s $ for the first half of the journey, i.e. from $ s = 0\;m $ to $ s = 60\;m $ .
The slope of the graph can be determined by dividing the $ Y $ axis coordinates with the $ X $ axis coordinates. Thus we get the slope as
 $ \dfrac{{15 - 3}}{{60 - 0}} = \dfrac{1}{5} $
Now considering the general $ Y $ axis coordinate as $ v $ and the $ X $ axis coordinate as $ s $ the equation of the line in slope point form will be
 $ \dfrac{{v - 3}}{{s - 0}} = \dfrac{1}{5} $
 $ \Rightarrow v = \dfrac{{s + 15}}{5} $
We know that
 $ v = \dfrac{{ds}}{{dt}} $
Substituting the value of $ v $ from the above equation, we get
 $ \dfrac{{ds}}{{dt}} = \dfrac{{s + 15}}{5} $
 $ \Rightarrow \dfrac{{ds}}{{s + 15}} = \dfrac{{dt}}{5} $
Now integrating both sides of the equation, we get,
 $ \Rightarrow \int {\dfrac{{ds}}{{s + 15}}} = \int {\dfrac{{dt}}{5}} $
Putting the limits of integration from $ s = 0\;m $ to $ s = 60\;m $ , we get,
 $ \Rightarrow \int\limits_{s = 0}^{s = 60} {\dfrac{{ds}}{{s + 15}}} = \int\limits_{t = 0}^{t = t} {\dfrac{{dt}}{5}} $
 $ \Rightarrow \left[ {\ln \;(s + 15)} \right]_0^{60} = \left[ {\dfrac{t}{5}} \right]_0^t $
Putting the values of the limits of the integration, we get,
 $ \Rightarrow \left[ {\ln \;(60 + 15) - \ln \;(0 + 15)} \right] = \left[ {\dfrac{t}{5} - \dfrac{0}{5}} \right] $
 $ \Rightarrow \left[ {\ln \;(75) - \ln \;(15)} \right] = \dfrac{t}{5} $
On further simplifying, we get,
 $ \Rightarrow \dfrac{t}{5} = \ln \left( {\dfrac{{75}}{{15}}} \right) $
 $ \Rightarrow \dfrac{t}{5} = \ln \left( 5 \right) $
 $ \Rightarrow t = 5 \times \ln \left( 5 \right) $
It is given in the question that $ \ln \;5 = 1.6 $ . Substituting this value in the above equation, we get,
 $ \Rightarrow t = 5 \times 1.6 $
 $ \Rightarrow t = 8\;\sec $
This is the time taken for the motorcycle to reach $ s = 60\;m $ .
Now for the next half of the journey, i.e. from $ s = 60\;m $ to $ s = 120\;m $ , we can repeat the above process.
We see that the velocity for this half of the journey is constant, i.e. $ v = 15\;m/s $ .
Using this uniform velocity, and the relation $ v = \dfrac{{ds}}{{dt}} $ , we get,
 $ v = 15\;m/s = \dfrac{{ds}}{{dt}} $
 $ \Rightarrow \dfrac{{ds}}{{dt}} = 15 $
 $ \Rightarrow ds = 15dt $
Integrating both sides, we get,
 $ \Rightarrow \int {ds} = \int {15dt} $
We now have to substitute the limits carefully. The displacement $ s $ will vary from $ s = 60\;m $ to $ s = 120\;m $ . The time taken $ t $ will vary from $ t = 8\;\sec $ to $ t = t $ , such that the value of the time $ t $ will give the actual time taken by the motorcycle to travel the entire distance of $ 120\;m $ .
 $ \Rightarrow \int\limits_{s = 60}^{s = 120} {ds} = \int\limits_{t = 8}^{t = t} {15dt} $
 $ \Rightarrow \left[ s \right]_{60}^{120} = \left[ {15t} \right]_8^t $
Now calculating the limits properly, we obtain,
 $ \Rightarrow \left[ {15{\mkern 1mu} (t - 8)} \right] = \left[ {120 - 60} \right] $
 $ \Rightarrow t - 8 = \dfrac{{60}}{{15}} $
Upon rearranging the equation we get,
 $ \Rightarrow t = 8 + 4 $
 $ \Rightarrow t = 12\;\sec $
It is given that this time is equal to $ 2\;x $ .
Therefore $ 2x = 12\;\sec $ .
 $ \Rightarrow x = 6 $
Thus the total time taken by the motorcycle to travel the entire distance of $ 120\;m $ is $ 12\;\sec $ with the value of $ x $ being $ 6 $ .

Note:
The motorcycle moves with some acceleration in the first half of the motion. In the second half of the motion, the acceleration of the motorcycle is $ 0 $ . Since the two graphs are two separate straight lines, we have analyzed them differently and have used the major relation $ v = \dfrac{{ds}}{{dt}} $ to simplify and integrate to get the solution.