Question

The upper half of an inclined plane of inclination $\theta $ is perfectly smooth while the lower half is rough. A block starting from rest at the top of the plane will again come to rest at the bottom if the coefficient of friction between the block and the lower half of the plane is given by.
\[\begin{align}
  & A.~~~~~~~\mu =2\tan \theta \\
 & B.~~~~~~~\mu =\tan \theta \\
 & C.~~~~~~~\mu =\dfrac{2}{\tan \theta } \\
 & D.~~~~~~~\mu =\dfrac{1}{\tan \theta } \\
\end{align}\]

Answer 1

Hint: Apply Newton’s law of motion separately for both the motions. Final velocity of the first half will be equal to initial velocity of the second half. Magnitude of displacement for both the motions is the same. As we are not asked about time, Newton’s third law of motion will be helpful.

Complete Step By Step Solution:
Let us assume mass of block be m kg, g be acceleration due to gravity, total length of incline l and velocity at halfway v. free body diagram of the block for first half,

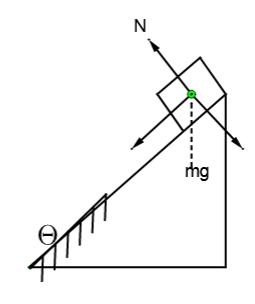
The acceleration of block will be along the incline and equal to
$a=\dfrac{mg\sin \theta }{m}=g\sin \theta $
As the acceleration is constant for the motion we can apply Newton’s law of motion
 Applying Newton’s third law of motion form starting to before reaching rough surface
${{v}^{2}}={{u}^{2}}+2as$
${{v}^{2}}={{0}^{2}}+2\left( g\sin \theta \right)\dfrac{l}{2}=gl\sin \theta $ … (1)
Now, free body diagram of the block for second half

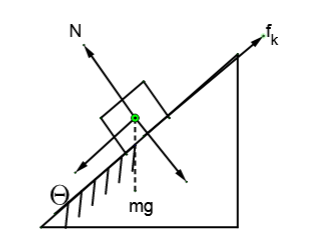
Here as the block is moving only along the incline, net force perpendicular to it must be zero. So,
$N=mg\cos \theta $
Also the block is sliding over incline, so friction will be
${{f}_{k}}=\mu N=\mu mg\cos \theta $
Acceleration of block will b along the incline will be
$\dfrac{mg\sin \theta -\mu mg\cos \theta }{m}=g\sin \theta -\mu g\cos \theta $

 As the acceleration is constant for the motion we can apply Newton’s law of motion
 Applying Newton’s third law of motion form starting of rough surface to bottom
${{v}^{2}}={{u}^{2}}+2as$
${{0}^{2}}={{v}^{2}}+2\left( g\sin \theta -\mu g\cos \theta \right)\dfrac{l}{2}$
Putting value of ${{v}^{2}}$ from equation 2 and solving we get
\[g\sin \theta =\left( \mu g\cos \theta -g\sin \theta \right)\]
$\mu =2\tan \theta $
Hence the correct option is A.

Note: This question can be solved with the following method. We know that both half motions are almost identical as initial velocity and final velocity has just got interchanged and length of both motions is the same too. So, we can say the magnitude of acceleration of both should be the same and the direction of acceleration of both should be opposite. So, we will get
$g\sin \theta -\mu g\cos \theta =-g\sin \theta $
$\mu =2\tan \theta $.