Question

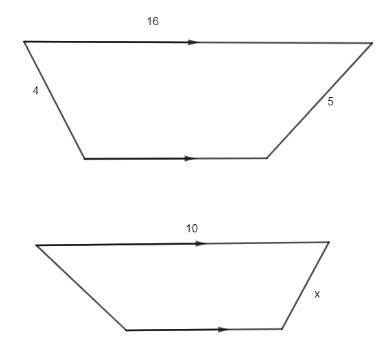
The two trapezoids are similar. What is the value of x?

A.2
B.2.5
C.3
D.3.125

Answer 1

Hint: In this problem small trapezium is a scalar version of larger trapezium it’s a mirror image. Hence, side x is corresponding to side 4 and side 10 corresponds to 16 and by cross multiplying this we get the value of x.

Complete answer:
Before going to the problem first of all we need to understand the concept of trapezium.
Trapezium has two parallel sides but length is unequal and also has two non-parallel sides but length is not equivalent.
Here, in this problem, two similar trapeziums are given from which we have found the length of the side in the second trapezium which is given as x.
There are two trapeziums in this question. The first one is larger and the second is smaller trapezium. If you observe the given diagram then you can see that the smaller trapezium is a scalar version of the larger trapezium, but is also a mirror image.
That means sides x corresponding to the length 4 on larger trapezium. Similarly, length 10 corresponds to length 16.
When we write in the form of expression then we get:
$\Rightarrow$ \[\dfrac{x}{4}=\dfrac{10}{16}\]
By cross multiplying this we get:
$\Rightarrow$ \[16x=40\]
Dividing by 16 both sides we get:
$\Rightarrow$ \[x=\dfrac{40}{16}\]
 By simplifying further, we get:
$\Rightarrow$ \[x=\dfrac{5}{2}\]
Therefore, we get the value of x that is
$\Rightarrow$ \[x=2.5\]
So, the correct option is “option B”.

Note:
Most of the students have misconception about trapezoids and trapeziums that they both are the same. But actually, they both are different. Because in British, trapezoid is defined as a quadrilateral with no parallel sides and trapezium is defined as a quadrilateral with one pair of parallel sides. The shape of trapezium is defined differently in different countries.