Question

The two horizontal lines shown in the above figure are parallel to each other. Which of the following does not equal to 180°.

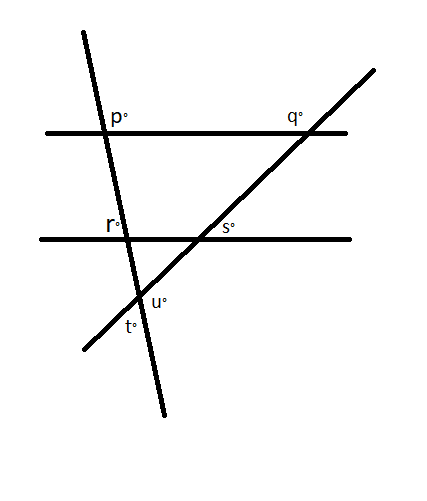
  A.$\;\;\;\;\;\;\left( {p + r} \right)^\circ \\$

  B.$\;\;\;\;\;\left( {p + t} \right)^\circ \\$

  C.$\;\;\;\;\;\left( {q + s} \right)^\circ \\$

  D.$\;\;\;\;\;\left( {r + s + t} \right)^\circ \\$

  E.$\;\;\;\;\;\;\left( {t + u} \right)^\circ \\ $

Answer 1

Hint: First we’ll find the pairs of corresponding angles, vertically opposite angles, and linear angle pairs to get some equation in the given variables. Also using the exterior angle property of a triangle, we get an equation. Using those equations substituting in the equation required to find the sum of which angles measures 180°.

Complete step by step answer:

Given data: The two horizontal lines are parallel.

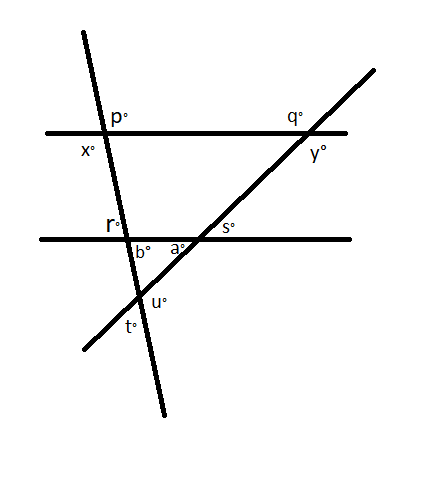
Using corresponding angles, because it is given that horizontal lines are parallel lines we can say
That, \[(x + r)^\circ = 180^\circ ...........(i)\]
And, \[(y + s)^\circ = 180^\circ ............(ii)\]
Using vertically opposite angles, we can say
That $x^\circ = p^\circ $
And, $q^\circ = y^\circ $
Substituting the value of x and y to the equation (i) and (ii), we get,
\[ \Rightarrow (p + r)^\circ = 180^\circ \]
\[ \Rightarrow (q + s)^\circ = 180^\circ \]
Using the exterior angle property of a triangle, i.e. exterior angle of a triangle is equal to the sum of the non-adjacent interior angles of the triangle. We can conclude
That \[(a + b)^\circ = u^\circ .............(iii)\]
Again Using vertically opposite angles, we can say
That $b^\circ = r^\circ $
And, $a^\circ = s^\circ $
Now substitute the value of a and b in equation(iii)
i.e. \[(r + s)^\circ = u^\circ \]
Now, using the linear pair i.e. sum of all angles lying on one side of a straight line measures 180°
i.e. \[(u + t)^\circ = 180^\circ ..........(iv)\]
Now substitute the value of u in equation(iv), we get,
i.e. \[(r + s + t)^\circ = 180^\circ \]
From the above equations, we can say that only (p+t)° does not measure 180°
therefore, option (B) is the correct option
Note: We know that in a triangle sum of all interior angles of a triangle measures 180° similarly the sum of all exterior angles of a triangle also measures 180°.
So here we can say
That \[(r + s + t)^\circ = 180^\circ \], that is giving us a similar equation as we’ve found in the above solution.