Question

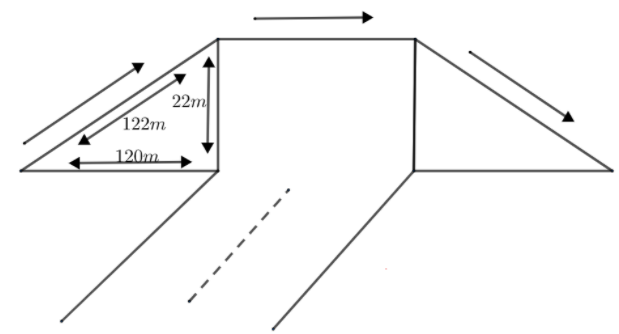
The triangular sidewall of the flyover has been used for the advertisement. The sides of the walls are 122m, 22m, and 120m. The advertisement yields an earning of Rs 5000 per ${{m}^{2}}$ per year. The company hired one of its walls for 3 months. How much rent did it pay?

a). Rs. 1650000
b). Rs. 1750000
c). Rs. 1600000
d). none of the above.

Answer 1

Hint: Before finding the rent paid by the company we will first find the area of the triangle used for the advertisement and then we will multiply the area with the Rs 5000 and the time for which the wall is hired in a year to get the required rent to be paid by the company.

Complete step-by-step solution:
Since from the question, we can see that the triangular side of the flyover is used for the advertisement. And, we have to find the rent paid by the company who has hired that one triangular wall for an advertisement for 3 months. But before that, we will find the area of the triangular wall which is used for the advertisement.
So, let us say that ABC is a triangle which is used for advertisement.

So, from the question we can say that AB = 120m, BC = 22m, and AC = 122m.
Since, we can see that ${{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( 120 \right)}^{2}}+{{\left( 22 \right)}^{2}}=14884$
And, ${{\left( AC \right)}^{2}}={{\left( 122 \right)}^{2}}=14884$
So, we can say that ${{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( AC \right)}^{2}}$
Hence, we can say that ABC is a right-angled triangle.
So, the area of the triangle ABC is equal to $\dfrac{1}{2}\times base\times height$ = $\dfrac{1}{2}\times AB\times AC$
So, area of $\Delta ABC$ = $\dfrac{1}{2}\times 120\times 22{{m}^{2}}$= $1320{{m}^{2}}$
Now, we can see from the question that the cost of advertisement on the triangular wall per year = Rs 5000 per ${{m}^{2}}$
So, we can say that cost of advertisement on the triangular wall per month = $Rs\dfrac{5000}{12}\text{per }{{m}^{2}}$
Now, we can say that cost of advertisement on the triangular wall for 3 months = $Rs\dfrac{5000}{12}\times \text{3 }{{m}^{2}}=Rs\dfrac{5000}{4}\text{ }{{m}^{2}}=Rs1250{{m}^{2}}$
So, cost of advertising the area of $1320{{m}^{2}}$ for 3 months $=Rs1250\times 1320=Rs1650000$
Hence, the rent which the company will pay is equal to Rs 1650000.
Hence, option (a) is the correct option.

Note: Students are required to note that they can also find the area of triangle directly here without proving triangle as right-angled triangle using Heron’s formula (i.e. $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ and here a, b, c are sides of the triangle and s is the semi perimeter of the triangle).