Question

The triangular side walls of a flyover have been used for advertisements. The sides of the walls are 122m, 22m, and 120m (see the given figure). The advertisements yield on earnings of 5000Rs. per ${m^2}$per year. A company hired one of its walls for 3 months. How much rent did it pay?

Answer 1

Hint: In order to deal with this question we will use the concept as the perimeter of a triangle is equal to the sum of its three sides and according to it we will find the semi perimeter of the triangle further by using heron's formula we will get the area of the wall and at last, by using given rate we will evaluate required rent paid by the company.

Complete step-by-step answer:

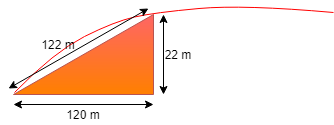
Let the sides of the triangle are a = 122m, b = 22m, c = 120m
As we know that perimeter of a triangle is equal to the sum of its three sides
So, semi perimeter of triangle =
$ \Delta s = (a + b + c)/2 $
$ = (122 + 22 + 120)/2 $
$ = 264/2 $
$ = 132 $
Now we will use Heron's formula to calculate the area of triangle
Therefore, Heron's formula is given as
$\sqrt {s(s - a)(s - b)(s - c)} $
Area of wall = $\sqrt {s(s - a)(s - b)(s - c)} $

Substitute obtained values in above formula we have
 $ \sqrt {s(s - a)(s - b)(s - c)} $
 $ = \sqrt {132(132 - 122)(132 - 22)(132 - 120)} $
 $ = \sqrt {132(10)(110)(12)} $
 $ = \sqrt {11 \times 12 \times 10 \times 11 \times 10 \times 12} $
 $ = \sqrt {11 \times 11 \times 12 \times 12 \times 10 \times 10} $
 $ = 11 \times 12 \times 10 $
 $ = 1320{m^2} $

It is given that earning on 1 ${m^2}$ per year = 5,000Rs.
So, Earning on 1320 ${m^2}$per year $ = 1320 \times 5000 = 6600000Rs.$

Now, earning in 1320 ${m^2}$ in 12 months = 6600000Rs.

Therefore, earning in 3 months = $\dfrac{{Rs.6600000 \times 3}}{{12}}$ = Rs. 1650000.

Hence, the rent paid by the company for 3 months is Rs. 1650000.

Note: In the above solution we used the concept of Heron’s formula which is used to calculate the area covered by a triangle which is given as $\sqrt {s(s - a)(s - b)(s - c)} $where a, b and c are the sides of a triangle and s shows the semi perimeter of a triangle which can be calculated by$\Delta s = (a + b + c)/2$.