Question

The triangles ∆RST ~ ∆UAY. In ∆RST, RS = 6 cm, ∠S = 50°, ST = 7.5 cm. The corresponding sides of ∆RST and ∆UAY are in the ratio 5: 4. Using this construct the triangle ∆UAY.

Answer 1

Hint: In order to construct the ∆UAY we need to find at least the lengths of two sides and the measure of one angle of the ∆UAY. We determine this data using the property of corresponding sides of similar triangles between ∆RST and ∆UAY. Dimensions of ∆RST are given.

Complete step-by-step answer:
Given Data,
∆RST ~ ∆UAY
In ∆RST, RS = 6 cm, ∠S = 50°, ST = 7.5 cm

Given that ∆RST ~ ∆UAY
In ∆RST, RS = 6 cm, ∠S = 50°, ST = 7.5 cm
Also given that the corresponding sides of ∆RST and ∆UAY are in the ratio 5: 4
$\therefore \dfrac{{{\text{RS}}}}{{{\text{UA}}}} = \dfrac{{{\text{ST}}}}{{{\text{AY}}}} = \dfrac{{{\text{RT}}}}{{{\text{UY}}}} = \dfrac{5}{4}$

We know by the property of common parts of similar triangles that the ratio of the corresponding sides of both triangles is equal, which implies the corresponding angles of both triangles are equal.
$ \Rightarrow \angle {\text{S = }}\angle {\text{A = 50}}^\circ $

Now, from the above
$\dfrac{{{\text{RS}}}}{{{\text{UA}}}} = \dfrac{5}{4}$
Given RS = 6 cm
$
   \Rightarrow \dfrac{6}{{{\text{UA}}}} = \dfrac{5}{4} \\
   \Rightarrow {\text{UA = }}\dfrac{4}{5} \times 6 \\
   \Rightarrow {\text{UA = 4}}{\text{.8 cm}} \\
$
Similarly, \[\dfrac{{{\text{ST}}}}{{{\text{AY}}}} = \dfrac{5}{4}\]
Given ST = 7.5 cm
$
   \Rightarrow \dfrac{{7.5}}{{{\text{AY}}}} = \dfrac{5}{4} \\
   \Rightarrow {\text{AY = }}\dfrac{4}{5} \times 7.5 \\
   \Rightarrow {\text{AY = 6 cm}} \\
$

There in ∆UAY, UA = 4.8 cm, ∠A = 50°, AY = 6 cm
Now we draw the triangle ∆UAY with the line segment first measuring 4.8 cm, then from one end of the line segment we measure the angle of 50° using a protractor. Now we draw another line segment of length 7.5 cm passing through this point and join the remaining side end to end.
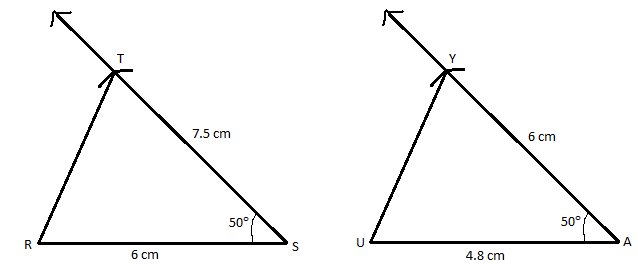
The figures of triangles ∆UAY and ∆RST looks as follows:

Note – In order to solve this type of problems the key is to know the concept of common parts of similar triangles. Similar triangles does not mean the lengths of their sides are equal by the lengths of corresponding sides are in a ratio and their corresponding angles are equal.
Once we’ve found the dimensions of the triangle to be drawn, we use geometric instruments to do this. We use a scale to measure the length and draw the sides of the triangle and a protractor to measure the angle. We should know how to use these geometrical instruments.