Question

The total surface area of an open pipe of length 50 cm, external diameter 20 cm and internal diameter 6 cm is approximately
$
  {\text{A}}{\text{. }}2787.84c{m^2} \\
  {\text{B}}{\text{. }}4655.84c{m^2} \\
  {\text{C}}{\text{. }}8693.84c{m^2} \\
  {\text{D}}{\text{. }}5742.84c{m^2} \\
 $

Answer 1

Hint: - Here we have to go through the formula of the curved surface area of the cylinder and we have to find the curved surface area two times: one for inner surface and one for outer surface and also for the remaining circular portion.

Complete step-by-step answer:

Here in the question it is given that a pipe with inner diameter 6 cm, outer diameter 20 cm and length 50 cm.
For better understanding we made the diagram of a pipe.

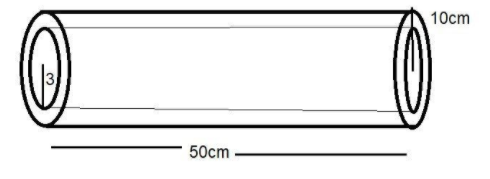
Now for inner curved surface we have,
Inner diameter =6 cm, so inner radius(r) $ = \dfrac{6}{2}cm = 3cm$
And the given length is the same for inner and outer radius i.e. length (h) =50cm.
As we know the formula of the curved surface area of the cylinder is$2\pi rh$.
Now put the values in the formula we get,
$ \Rightarrow 2\pi rh = 2 \times \dfrac{{22}}{7} \times 3 \times 50c{m^2}$
Now we solve similarly for outer curved surface,
Outer diameter =6 cm, so outer radius(R) $ = \dfrac{{20}}{2}cm = 10cm$
Now put the values in the formula of curved surface area we get,
$ \Rightarrow 2\pi Rh = 2 \times \dfrac{{22}}{7} \times 10 \times 50c{m^2}$
And now we have to find the area of remaining circular portion for that we simply subtract the inner circular area through the outer circular area i.e. $2\pi {R^2} - 2\pi {r^2} = 2\pi ({R^2} - {r^2})$
Now put the values in the above formula we get,
$ \Rightarrow 2\pi ({R^2} - {r^2}) = 2\pi ({10^2} - {3^2}) = 2 \times \dfrac{{22}}{7} \times 91c{m^2}$
Now for total surface area of pipe we have to add all the area we calculated above i.e.
Total surface area of pipe = Curved surface area of inner pipe + curved surface area of outer pipe + Area of remaining circular portion
$
   = 2 \times \dfrac{{22}}{7} \times 3 \times 50c{m^2} + 2 \times \dfrac{{22}}{7} \times 10 \times 50c{m^2} + 2 \times \dfrac{{22}}{7} \times 91c{m^2} \\
   = 2 \times \dfrac{{22}}{7}\left( {150 + 500 + 91} \right)c{m^2} \\
   = 1482 \times \dfrac{{22}}{7}c{m^2} \\
   = 4655.84c{m^2} \\
 $

Hence option B is the correct answer.

Note: - Whenever we face such a type of question we have to calculate the area one by one of each to find out the total surface area at the end. We should also draw the diagram for better understanding. And then apply the formula of that surface whose area we have to calculate. There is a chance that students forget to take the area of circles as well so please take care of that when asked for total surface area.