Question

The top of a 15m high tower makes an angle of elevation of $60{}^\circ $ with the bottom of an electric pole and an angle of elevation of $30{}^\circ $ with the top of the pole. What is the height of the electric pole?
[a] 5m
[b] 8m
[c] 10m
[d] 12m

Answer 1

Hint: Use the fact that $\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}$. Find tan of angle D in triangle BDA and use the fact that $\tan 60{}^\circ =\sqrt{3}$. Hence find the length of the side AD. Again find tan if angle E in triangle BEF and use the fact that $\tan 30{}^\circ =\sqrt{3}$ and hence find the length of the side BF. Use the fact that ED = AB – BF to determine the height of the tower.

Complete step-by-step answer:

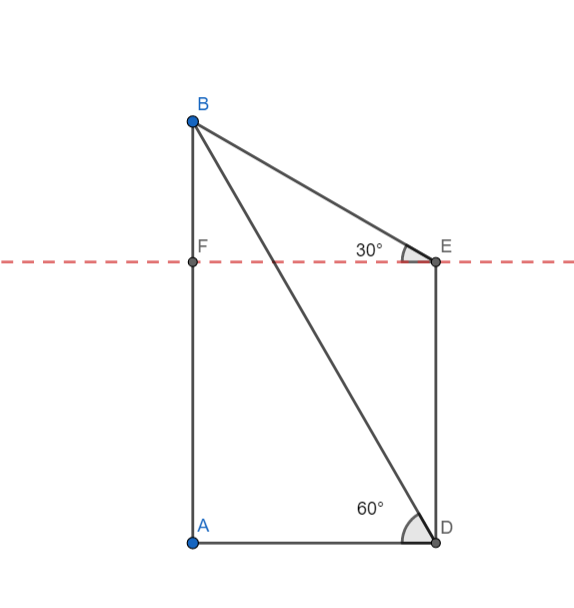
AB is a tower of height 15m. ED is an electric pole at a distance from the tower, The angle of elevation from the top(E) of the pole to the top(B) of the tower is $30{}^\circ $ , and the angle of elevation of the bottom(D) of the pole to the top(B) of the tower is $60{}^\circ $.
To find: The height of the pole ED.
In triangle ABD, we have AB is the side opposite to D and AD is the side adjacent to D.
We know that $\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}$
Hence, we have
$\tan D=\dfrac{AB}{AD}$
We know that $AB=15,D=60{}^\circ $
Hence, we have
$\tan 60{}^\circ =\dfrac{15}{AD}$
We know that $\tan 60{}^\circ =\sqrt{3}$
Hence, we have $\sqrt{3}=\dfrac{15}{AD}$
Multiplying both sides by AD, we get
$\sqrt{3}AD=15$
Dividing both sides by $\sqrt{3},$ we get
$AD=\dfrac{15}{\sqrt{3}}=5\sqrt{3}$
Since ADEF is a rectangle, we have AD = EF.
Hence, we have $EF=5\sqrt{3}$
Now, in triangle BEF, we have
BF is the side opposite to E, and FE is the side adjacent to E.
We know that $\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}$
Hence, we have
$\tan E=\dfrac{BF}{FE}$
We know that $EF=5\sqrt{3}$ and $E=30{}^\circ $
Hence, we have
$\tan 30{}^\circ =\dfrac{BF}{5\sqrt{3}}$
We know that $\tan 30{}^\circ =\dfrac{1}{\sqrt{3}}$
Hence, we have
$\dfrac{1}{\sqrt{3}}=\dfrac{BF}{5\sqrt{3}}$
Multiplying both sides by $5\sqrt{3}$, we get
$BF=5$
Now, we know that
BF+FA = AB
Since ADEF is a rectangle, we have AF = ED
Hence, we have
BF+ED = AB
ED + 5 = 15
Subtracting 5 from both sides, we get
ED = 10
Hence the height of the pole is 10m.
Hence option [c] is correct.

Note: Verification:
In triangle BEF, we have
$\tan E=\dfrac{BF}{EF}=\dfrac{5}{5\sqrt{3}}=\dfrac{1}{\sqrt{3}}$
Hence, we have
$\tan E=\tan 30{}^\circ \Rightarrow E=30{}^\circ $
Hence the angle of elevation of the top of the tower from the top of the pole is $30{}^\circ $
In triangle ABD, we have
$\tan D=\dfrac{AB}{AD}=\dfrac{15}{5\sqrt{3}}=\sqrt{3}\Rightarrow D=60{}^\circ $
Hence the angle of elevation of the top of the tower from the bottom of the pole is $60{}^\circ $
Hence our answer is verified to be correct.