Question

The tidal waves in the sea are primarily due to:
A. The gravitational effect of the moon on the earth
B. The gravitational effect of the sun on the earth
C. The gravitational effect of the Venus on the earth
D. The atmospheric effect of the earth itself.

Answer 1

Hint: The gravitational force varies with respect to the square of the distance between two objects.
Newton’s gravitational law is given by -
\[F=G\dfrac{{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\] …………(1)
Where, G is the gravitational constant
                    \[{{m}_{1}}\] is the mass of the first object,
                    \[{{m}_{2}}\] is the mass of the second object,
              r is the distance between two objects.
Determine the dependence of gravitational pull on a particle on the surface of earth. Compare the value between moon and sun. Moon will show a stronger effect.

Complete answer:
Gravitational force is a universal force, and it acts between any two objects.
If we consider one of the objects to be the same (Water molecules on the surface of earth in this case), then the variables are the mass of the second object and the distance between the objects.
So, we need to focus on the following quantity,
\[\dfrac{{{m}_{2}}}{{{r}^{2}}}\]
Mass of the sun is almost $27\times {{10}^{6}}$ times the mass of the moon.
However, we need to consider the distance of the sun and moon to get the complete picture.
Distance from sun to earth is around 150 million kilometers.
But the distance between earth and moon is only \[3\times {{10}^{5}}km\] .
As the gravitational force is inversely proportional to the square of the distance, the effect of is less than the sun. i.e.
 \[{{F}_{g}}\propto \dfrac{m}{{{r}^{2}}}\]

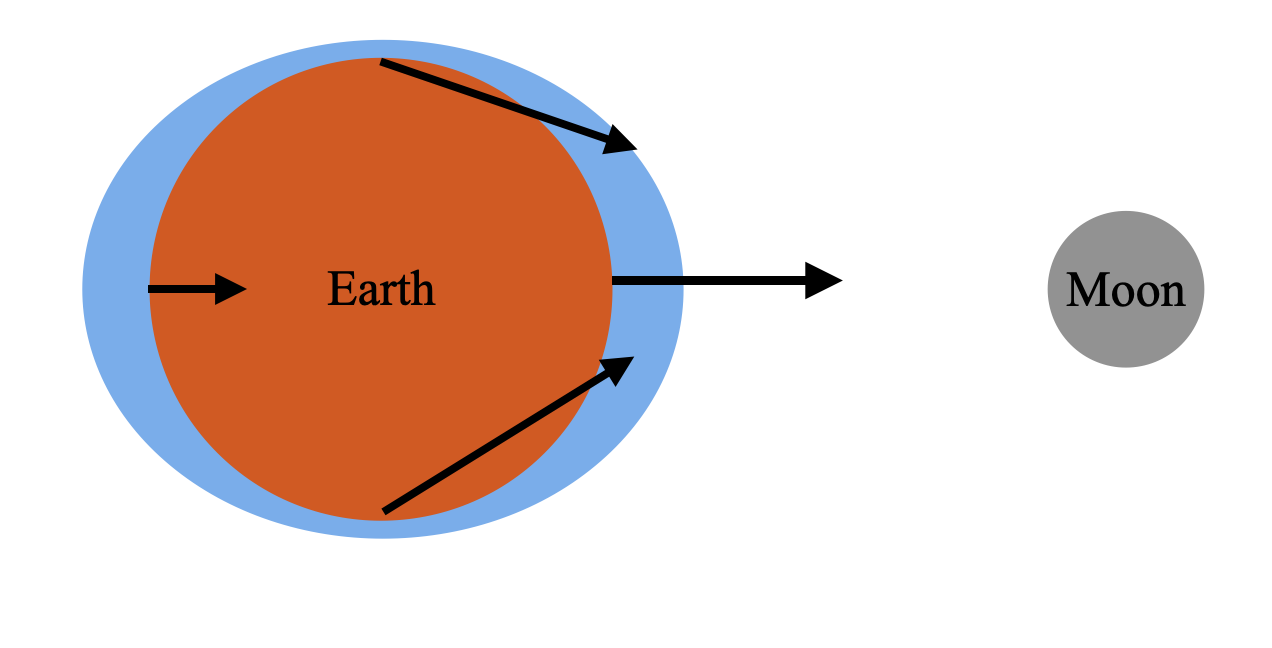
Mass of the sun is much greater than the mass of the moon. Also the distance to sun from earth is that much greater that of to the moon. From the gravitational force equation we can see that it is inversely proportional to the square of distance.
That is, \[\dfrac{1}{{{r}_{moon}}^{2}}\gg \dfrac{1}{{{r}_{sun}}^{2}}\].
Therefore, \[{{F}_{moon}}\gg {{F}_{sun}}\].
The following figure shows the effect more accurately.

So, the correct answer is “Option A”.

Note:
As the gravitational force is a universal force, sun tides also exist. However, the intensity of the sun tides increases when it aligns with the moon. That is why the tides on New Moon and Full Moon become more apparent. When you have to answer a theoretical question with the help of a formula, you need to consider all the variables that are changing between the two comparable objects. For example, in this case, we considered both mass and distance.