The tangent of the curve $y={{x}^{2}}+6$ at a point $\left( 1,7 \right)$ touches the circle ${{x}^{2}}+{{y}^{2}}+16x+12y+c=0$ at Q. Find the coordinates of Q?
Answer
Verified629.4k+ views
Hint: We start solving the by finding the slope of the tangent to the curve $y={{x}^{2}}+6$ at the point $\left( 1,7 \right)$. We then find the equation of the tangent using the slope that we have just obtained. Using this equation of the tangent, we find the value of c in the equation of the circle given using the fact that the perpendicular distance from center to the tangent in a circle is equal to the radius of the circle. We then substitute the equation of tangent in the circle and make subsequent calculations to get the required coordinates of the circle.
Complete step by step answer:
According to the problem, we have a tangent to the curve $y={{x}^{2}}+6$ at the point $\left( 1,7 \right)$ touches the circle ${{x}^{2}}+{{y}^{2}}+16x+12y+c=0$ at Q. We need to find the coordinates of the point Q.
Let us draw the given information to get a better view.
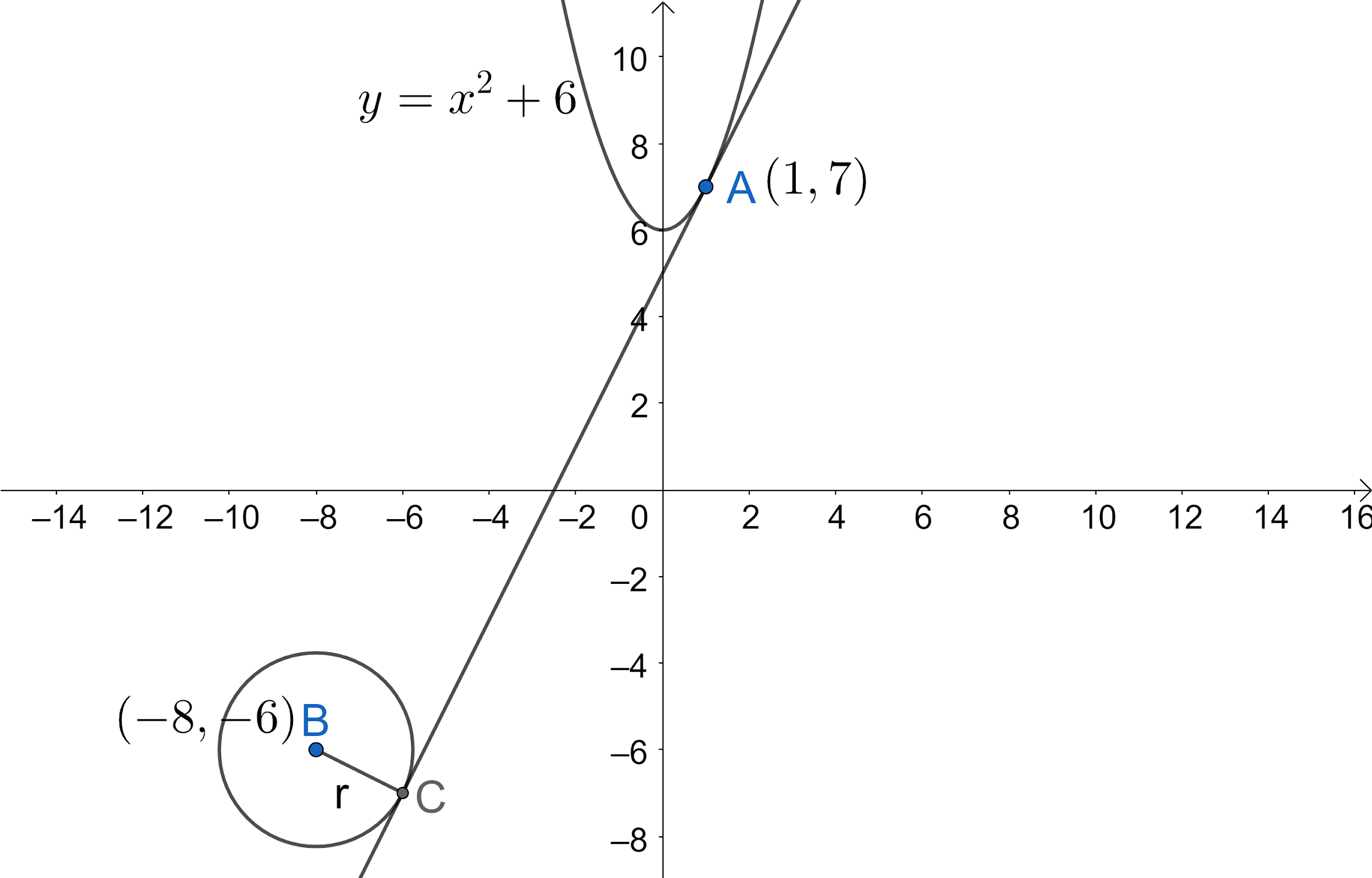
We know that slope of tangent to any curve y at the given point $P\left( {{x}_{1}},{{y}_{1}} \right)$ is ${{\left. \dfrac{dy}{dx} \right|}_{P\left( {{x}_{1}},{{y}_{1}} \right)}}$.
Let us find the slope of the tangent to the curve $y={{x}^{2}}+6$ at the point $\left( 1,7 \right)$.
We have $y={{x}^{2}}+6$. Let us differentiate it with respect to x on both sides.
$\Rightarrow \dfrac{dy}{dx}=\dfrac{d}{dx}\left( {{x}^{2}}+6 \right)$.
We know that $\dfrac{d}{dx}\left( f\left( x \right)+g\left( x \right) \right)=\dfrac{d}{dx}\left( f\left( x \right) \right)+\dfrac{d}{dx}\left( g\left( x \right) \right)$.
$\Rightarrow \dfrac{dy}{dx}=\dfrac{d}{dx}\left( {{x}^{2}} \right)+\dfrac{d}{dx}\left( 6 \right)$.
We know that $\dfrac{d}{dx}\left( {{x}^{n}} \right)=n{{x}^{n-1}}$ and $\dfrac{d}{dx}\left( a \right)=0$.
$\Rightarrow \dfrac{dy}{dx}=2x+0$.
$\Rightarrow \dfrac{dy}{dx}=2x$.
Let us substitute the point $\left( 1,7 \right)$.
$\Rightarrow {{\left. \dfrac{dy}{dx} \right|}_{\left( 1,7 \right)}}=2\left( 1 \right)$.
$\Rightarrow {{\left. \dfrac{dy}{dx} \right|}_{\left( 1,7 \right)}}=2$.
We have got the slope of the tangent to the curve $y={{x}^{2}}+6$ at the point $\left( 1,7 \right)$ as 2.
Now, we find the equation of the tangent with slope 2 and passing through the point $\left( 1,7 \right)$.
We know that the equation of the line passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$ and having slope m is $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$.
The equation of the tangent is $y-7=2\left( x-1 \right)$.
$\Rightarrow y-7=2x-2$.
$\Rightarrow 2x-2-y+7=0$.
$\Rightarrow 2x-y+5=0$ ---(1).
The equation of the tangent is $2x-y+5=0$.
Now, we find the center and radius of the given circle ${{x}^{2}}+{{y}^{2}}+16x+12y+c=0$.
$\Rightarrow {{x}^{2}}+16x+64+{{y}^{2}}+12y+36-64-36+c=0$.
$\Rightarrow {{\left( x+8 \right)}^{2}}+{{\left( y+6 \right)}^{2}}-100+c=0$.
$\Rightarrow {{\left( x+8 \right)}^{2}}+{{\left( y+6 \right)}^{2}}=100-c$.
$\Rightarrow {{\left( x-\left( -8 \right) \right)}^{2}}+{{\left( y-\left( -6 \right) \right)}^{2}}={{\left( \sqrt{100-c} \right)}^{2}}$.
We know that if the equation of the circle is defined as ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$, then the center and radius of the circle is $\left( a,b \right)$ and r.
So, we have got the center and radius of the circle ${{x}^{2}}+{{y}^{2}}+16x+12y+c=0$ as $\left( -8,-6 \right)$ and $\sqrt{100-c}$ ---(2).
We know that the perpendicular distance from center to the tangent in a circle is equal to the radius of the circle.
We know that the perpendicular distance from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the line $ax+by+c=0$ is $\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$.
So, we have radius (r) = perpendicular distance from the point $\left( -8,-6 \right)$ to the tangent $2x-y+5=0$.
$\Rightarrow \sqrt{100-c}=\dfrac{\left| 2\left( -8 \right)-\left( -6 \right)+5 \right|}{\sqrt{{{2}^{2}}+{{\left( -1 \right)}^{2}}}}$.
$\Rightarrow \sqrt{100-c}=\dfrac{\left| -16+6+5 \right|}{\sqrt{4+1}}$.
$\Rightarrow \sqrt{100-c}=\dfrac{\left| -5 \right|}{\sqrt{5}}$.
$\Rightarrow \sqrt{100-c}=\dfrac{5}{\sqrt{5}}$.
$\Rightarrow \sqrt{100-c}=\sqrt{5}$.
Now, we square on both sides.
$\Rightarrow {{\left( \sqrt{100-c} \right)}^{2}}={{\left( \sqrt{5} \right)}^{2}}$.
$\Rightarrow 100-c=5$.
$\Rightarrow 100-5=c$.
$\Rightarrow c=95$.
So, we got the equation of the circle as ${{x}^{2}}+{{y}^{2}}+16x+12y+95=0$ ---(3).
From equation (1), we have the equation of tangent as $2x-y+5=0$.
$\Rightarrow y=2x+5$ ---(4).
We substitute equation (4) in equation (3).
$\Rightarrow {{x}^{2}}+{{\left( 2x+5 \right)}^{2}}+16x+12\left( 2x+5 \right)+95=0$.
$\Rightarrow {{x}^{2}}+4{{x}^{2}}+20x+25+16x+24x+60+95=0$.
$\Rightarrow 5{{x}^{2}}+60x+180=0$.
$\Rightarrow {{x}^{2}}+12x+36=0$.
\[\Rightarrow {{\left( x+6 \right)}^{2}}=0\].
\[\Rightarrow x+6=0\].
\[\Rightarrow x=-6\] ---(5).
We substitute equation (5) in equation (4).
$\Rightarrow y=2\left( -6 \right)+5$.
$\Rightarrow y=-12+5$.
$\Rightarrow y=-7$ ---(6).
From (5) and (6), we have coordinates of the Q as $\left( -6,-7 \right)$.
∴ The coordinates of the Q are $\left( -6,-7 \right)$.
Note: We can also find the coordinates of the point of contact by finding the point of intersection of tangent $2x-y+5=0$ and the line passing through the center of the circle and the point of contact (which is normal here). We should know that the point at which we find the slope lies on both the curve and the tangent. Similarly, we can also expect to find the normal for the given tangent, the point that lies on the opposite side of the diameter which has one endpoint as the point of contact we just obtained.
Complete step by step answer:
According to the problem, we have a tangent to the curve $y={{x}^{2}}+6$ at the point $\left( 1,7 \right)$ touches the circle ${{x}^{2}}+{{y}^{2}}+16x+12y+c=0$ at Q. We need to find the coordinates of the point Q.
Let us draw the given information to get a better view.
We know that slope of tangent to any curve y at the given point $P\left( {{x}_{1}},{{y}_{1}} \right)$ is ${{\left. \dfrac{dy}{dx} \right|}_{P\left( {{x}_{1}},{{y}_{1}} \right)}}$.
Let us find the slope of the tangent to the curve $y={{x}^{2}}+6$ at the point $\left( 1,7 \right)$.
We have $y={{x}^{2}}+6$. Let us differentiate it with respect to x on both sides.
$\Rightarrow \dfrac{dy}{dx}=\dfrac{d}{dx}\left( {{x}^{2}}+6 \right)$.
We know that $\dfrac{d}{dx}\left( f\left( x \right)+g\left( x \right) \right)=\dfrac{d}{dx}\left( f\left( x \right) \right)+\dfrac{d}{dx}\left( g\left( x \right) \right)$.
$\Rightarrow \dfrac{dy}{dx}=\dfrac{d}{dx}\left( {{x}^{2}} \right)+\dfrac{d}{dx}\left( 6 \right)$.
We know that $\dfrac{d}{dx}\left( {{x}^{n}} \right)=n{{x}^{n-1}}$ and $\dfrac{d}{dx}\left( a \right)=0$.
$\Rightarrow \dfrac{dy}{dx}=2x+0$.
$\Rightarrow \dfrac{dy}{dx}=2x$.
Let us substitute the point $\left( 1,7 \right)$.
$\Rightarrow {{\left. \dfrac{dy}{dx} \right|}_{\left( 1,7 \right)}}=2\left( 1 \right)$.
$\Rightarrow {{\left. \dfrac{dy}{dx} \right|}_{\left( 1,7 \right)}}=2$.
We have got the slope of the tangent to the curve $y={{x}^{2}}+6$ at the point $\left( 1,7 \right)$ as 2.
Now, we find the equation of the tangent with slope 2 and passing through the point $\left( 1,7 \right)$.
We know that the equation of the line passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$ and having slope m is $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$.
The equation of the tangent is $y-7=2\left( x-1 \right)$.
$\Rightarrow y-7=2x-2$.
$\Rightarrow 2x-2-y+7=0$.
$\Rightarrow 2x-y+5=0$ ---(1).
The equation of the tangent is $2x-y+5=0$.
Now, we find the center and radius of the given circle ${{x}^{2}}+{{y}^{2}}+16x+12y+c=0$.
$\Rightarrow {{x}^{2}}+16x+64+{{y}^{2}}+12y+36-64-36+c=0$.
$\Rightarrow {{\left( x+8 \right)}^{2}}+{{\left( y+6 \right)}^{2}}-100+c=0$.
$\Rightarrow {{\left( x+8 \right)}^{2}}+{{\left( y+6 \right)}^{2}}=100-c$.
$\Rightarrow {{\left( x-\left( -8 \right) \right)}^{2}}+{{\left( y-\left( -6 \right) \right)}^{2}}={{\left( \sqrt{100-c} \right)}^{2}}$.
We know that if the equation of the circle is defined as ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$, then the center and radius of the circle is $\left( a,b \right)$ and r.
So, we have got the center and radius of the circle ${{x}^{2}}+{{y}^{2}}+16x+12y+c=0$ as $\left( -8,-6 \right)$ and $\sqrt{100-c}$ ---(2).
We know that the perpendicular distance from center to the tangent in a circle is equal to the radius of the circle.
We know that the perpendicular distance from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ to the line $ax+by+c=0$ is $\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$.
So, we have radius (r) = perpendicular distance from the point $\left( -8,-6 \right)$ to the tangent $2x-y+5=0$.
$\Rightarrow \sqrt{100-c}=\dfrac{\left| 2\left( -8 \right)-\left( -6 \right)+5 \right|}{\sqrt{{{2}^{2}}+{{\left( -1 \right)}^{2}}}}$.
$\Rightarrow \sqrt{100-c}=\dfrac{\left| -16+6+5 \right|}{\sqrt{4+1}}$.
$\Rightarrow \sqrt{100-c}=\dfrac{\left| -5 \right|}{\sqrt{5}}$.
$\Rightarrow \sqrt{100-c}=\dfrac{5}{\sqrt{5}}$.
$\Rightarrow \sqrt{100-c}=\sqrt{5}$.
Now, we square on both sides.
$\Rightarrow {{\left( \sqrt{100-c} \right)}^{2}}={{\left( \sqrt{5} \right)}^{2}}$.
$\Rightarrow 100-c=5$.
$\Rightarrow 100-5=c$.
$\Rightarrow c=95$.
So, we got the equation of the circle as ${{x}^{2}}+{{y}^{2}}+16x+12y+95=0$ ---(3).
From equation (1), we have the equation of tangent as $2x-y+5=0$.
$\Rightarrow y=2x+5$ ---(4).
We substitute equation (4) in equation (3).
$\Rightarrow {{x}^{2}}+{{\left( 2x+5 \right)}^{2}}+16x+12\left( 2x+5 \right)+95=0$.
$\Rightarrow {{x}^{2}}+4{{x}^{2}}+20x+25+16x+24x+60+95=0$.
$\Rightarrow 5{{x}^{2}}+60x+180=0$.
$\Rightarrow {{x}^{2}}+12x+36=0$.
\[\Rightarrow {{\left( x+6 \right)}^{2}}=0\].
\[\Rightarrow x+6=0\].
\[\Rightarrow x=-6\] ---(5).
We substitute equation (5) in equation (4).
$\Rightarrow y=2\left( -6 \right)+5$.
$\Rightarrow y=-12+5$.
$\Rightarrow y=-7$ ---(6).
From (5) and (6), we have coordinates of the Q as $\left( -6,-7 \right)$.
∴ The coordinates of the Q are $\left( -6,-7 \right)$.
Note: We can also find the coordinates of the point of contact by finding the point of intersection of tangent $2x-y+5=0$ and the line passing through the center of the circle and the point of contact (which is normal here). We should know that the point at which we find the slope lies on both the curve and the tangent. Similarly, we can also expect to find the normal for the given tangent, the point that lies on the opposite side of the diameter which has one endpoint as the point of contact we just obtained.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success
Master Class 11 Social Science: Engaging Questions & Answers for Success
Master Class 11 Maths: Engaging Questions & Answers for Success
Master Class 11 Biology: Engaging Questions & Answers for Success
Master Class 11 Physics: Engaging Questions & Answers for Success
Master Class 11 Chemistry: Engaging Questions & Answers for Success
Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE
Difference Between Prokaryotic Cells and Eukaryotic Cells
Find the value of the expression given below sin 30circ class 11 maths CBSE
Difference between physical and chemical change class 11 chemistry CBSE
Two of the body parts which do not appear in MRI are class 11 biology CBSE
Draw a diagram of a plant cell and label at least eight class 11 biology CBSE