Question

The surface area of the solid of revolution of the region bounded by y = 2x, x =0 and x = 2 about x-axis is,
a. \[8\sqrt{5}\pi \]
b. \[2\sqrt{5}\pi \]
c. \[\sqrt{5}\pi \]
d. \[4\sqrt{5}\pi \]

Answer 1

Hint: Draw the rough figure according to the boundaries which we get a triangle. Imagine the solid formed by revolving the base of the triangle. Find the surface area of the solid formed.

Complete step-by-step answer:
Given us three equations, y = 2x, x = 0 and x = 2. Now let us mark these points in a Cartesian plane.
Given, y = 2x.
By substituting x = 0, we get y = 0.
If x =2, we get, \[y=2\times 2=4\].
Thus we have three points (0, 0), (2, 4) and (2, 0).

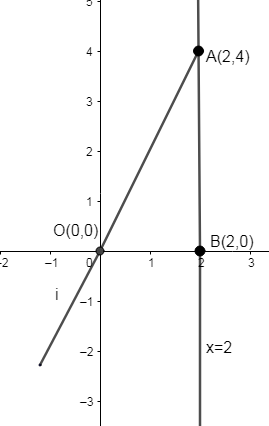
\[\because \] x = 2 where y = 0 thus forms point (2, 0).
Let us take (2, 4), as coordinates of A.

Similarly, we can say that B (2, 0) and O (0, 0).

Now this figure we got \[\vartriangle AOB\] becomes a right angled isosceles triangle, which is right angled at B.

The base of the triangle is 2 units along the x-axis and 4 units perpendicular to the x-axis.

A surface of revolution is a surface in Euclidean space created by rotating a curve around an axis of rotation.

The example of surfaces of revolution generated by the straight line are cylindrical and conical surfaces. A circle rotated around any diameter sphere.

Now if we rotate the triangle AOB about its base BO, then we may get a cone centered at B. So the base radius will be SB = 2 units, radius is represented as r. Thus, r = 4 units.

Similarly, height h = 2 units.

Therefore we need to find the curved surface area of the cone formed by surface revolution of triangle AOB.

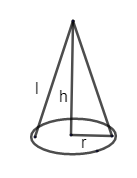
From the figure, l is the slant height.
We know, in a cone, \[{{l}^{2}}={{r}^{2}}+{{h}^{2}}\]
\[\therefore l=\sqrt{{{r}^{2}}+{{h}^{2}}}\]

The curved surface area of cone, \[S=\pi rl\]
\[S=\pi r\sqrt{{{r}^{2}}+{{h}^{2}}}\]

Substitute \[l=\sqrt{{{r}^{2}}+{{h}^{2}}}\] in the surface area of a cone.
\[\therefore S=\pi r\sqrt{{{r}^{2}}+{{h}^{2}}}\]

And here, S = surface area of cone. Put r = 4 units, h =2 units.
\[\begin{align}
  & S=\pi \left( 2 \right)\sqrt{{{2}^{2}}+{{4}^{2}}} \\
 & S=2\pi \sqrt{4+16}=2\pi \sqrt{20} \\
 & S=2\pi \sqrt{2\times 10}=2\pi \sqrt{2\times 2\times 5} \\
\end{align}\]
\[S=4\pi \sqrt{5}\] Sq. unit.
\[\therefore \] The curved surface area of the cone = \[4\pi \sqrt{5}\] Sq. unit.

Thus option (d) is the correct answer.

Note: In the question it's not mentioned to find the curved surface area of a cone. We need to find the solid formed from the rotation of the base of a triangle. Imagine the triangle rotating about its base and form the solid.