Question

The supply voltage to a room is 120 V. The resistance of the lead wires is 6 $\Omega $. A 60 W, 120 V bulb is already switched on. What is the decrease of voltage (in volts) across the bulb, when a 240 W, 120 V heater is switched on in parallel to the bulb?
A. 2.9
B. 13.3
C. 10.4
D. 0

Answer 1

Hint: First, we need to calculate the resistances of the bulb and the heater, and also find their equivalent resistance in parallel combination. Then by comparing the initial voltage drop for bulb and subtracting the voltage drop after connecting the heater, we can get the required answer.
Formula used:
The power consumed by a circuit is given in the terms of the voltage, the resistance and the current by the following expression.
$P = VI = \dfrac{{{V^2}}}{R}$

Complete answer:
Let us first consider the case of the bulb which is switched on in the room. Its rating is 60W, 120V. Therefore, for the bulb we have
$
  V = 120V \\
  P = 60W \\
 $
From this information we can find out the resistance of the bulb which is given as ${R_b} = \dfrac{{{V^2}}}{P} = \dfrac{{{{\left( {120} \right)}^2}}}{{60}} = 240\Omega $
Doing the same thing in the case of heater, we have the rating as 240 W, 120 V. Therefore, the resistance of the heater is
${R_h} = \dfrac{{{{\left( {120} \right)}^2}}}{{240}} = 60\Omega $
The bulb and the heater are connected in parallel so their resultant resistance is given as
$R = \dfrac{{{R_b}{R_h}}}{{{R_b} + {R_h}}} = \dfrac{{240 \times 60}}{{240 + 60}} = 48\Omega $

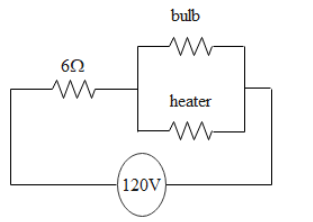
Before connecting the heater to the circuit, the potential drop across the bulb is given as
${V_1} = \dfrac{{{R_b}}}{{{R_b} + 6}} \times V = \dfrac{{240}}{{240 + 6}} \times 120 = 117.07V$
The resistance of the lead wires is 6 $\Omega $.
After we connect the heater to the circuit, the potential drop across the parallel combination of bulb and the heater is given as
${V_2} = \dfrac{R}{{R + 6}} \times V = \dfrac{{48}}{{48 + 6}} \times 120 = 106.67V$
Therefore, change in voltage is given as
${V_1} - {V_2} = 117.07 - 106.67 = 10.4V$

Hence, the correct answer is option C.

Note:
It should be noted that when only the bulb is connected to the circuit then it is in series with the resistance of the wires. When the heater is attached to the circuit, the parallel combination ensures that the voltage remains the same for bulb and heater.