Question

The supplementary angle of $120^\circ $is:
$\left( A \right)30^\circ $
$\left( B \right)50^\circ $
$\left( C \right)240^\circ $
$\left( D \right)60^\circ $

Answer 1

Hint: Here given, to find the supplementary angle we have to know the definition that is, the two angles are said to be supplementary when the addition of them is $180^\circ $. They don’t have to be next to each other, just as long as they can form the sum $180^\circ $.

Complete step-by-step solution:
By the definition of supplementary angles to find the supplementary angle of $120^\circ $,
Let $x$ be the supplementary angle of $120^\circ $,
Therefore,
$ \Rightarrow 120^\circ + x = 180^\circ $
$\begin{align}
  &\Rightarrow x = 180^\circ - 120^\circ \\
 &\Rightarrow x = 60^\circ . \\
\end{align} $

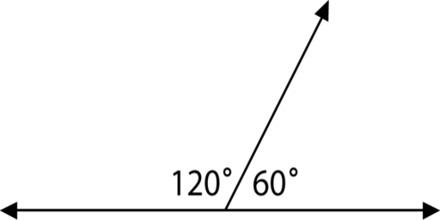
Therefore $60^\circ $ is the supplementary angle of $120^\circ $.

Note: Only two angles can sum to $180^\circ $, three or more angles may sum to $180^\circ $ or $\pi $radians, but they are not considered supplementary.
The two angles must either both be right angles, or either one of them must be acute angle and other must be obtuse angle. Supplementary angles sharing a common side will form a straight line.