Question

The sum of the measures of the interior angles of a convex polygon is \[{3060^ \circ }\]. How do you classify the polygon by the number of sides?

Answer 1

Hint:In the question, given that, the sum of the measures of the interior angles of a convex polygon. We are asked to classify the number of sides of a polygon. We can determine its number of sides by equating the sum of measure of the interior angles with the formula for calculating the sum of the interior angles.
\[(n - 2) \times {180^ \circ }\] Where n= number of sides of a polygon.

Complete step by step solution:
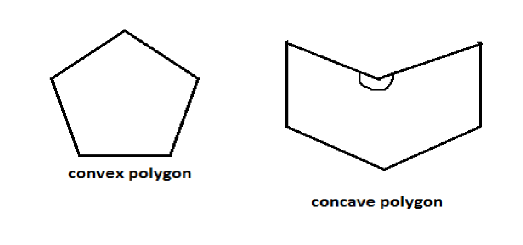
Firstly we should know what actually a convex polygon is. A Polygon is a closed figure having multiple sides. It can be regular or irregular. Polygon is basically categorized in two types on the basis of measure of interior angles:
(I) Convex polygon
(II) Concave polygon
Now, convex polygon is a polygon in which all the interior angles of a polygon should be less than\[{180^\circ }\].
For example, triangle, square etc.
Concave polygon is a polygon in which at least one interior angle is greater than \[{180^ \circ }\].

We are given that the sum of the measures of the interior angles of a convex polygon is \[{3060^ \circ}\].
Since, we already know the formula for calculating the sum of interior angles of a polygon is:
\[(n - 2) \times {180^ \circ }\] Where n= number of sides of a polygon.
Now, we don’t know the number of sides in this polygon, but we can determine its number of sides by equating the sum of measure of the interior angles with the formula for calculating the sum of the interior angles.
\[ \Rightarrow (n - 2) \times {180^ \circ } = {3060^ \circ }\]
Change the side of 180 from LHS to RHS along with change in sign.
\[ \Rightarrow (n - 2) = \dfrac{{{{3060}^ \circ }}}{{{{180}^ \circ }}}\]
\[
\Rightarrow (n - 2) = {17^ \circ } \\
\Rightarrow n - 2 = 17 \\
\]
Shifting constants to one side, we get
\[
\Rightarrow n = 17 + 2 \\
\Rightarrow n = 19 \\
\]
Therefore, the number of sides are 19 in the polygon whose sum of all the interior angles is\[{3060^\circ }\].
Formula used: The sum of interior angles of a polygon is:
\[(n - 2) \times {180^ \circ }\] Where n= number of sides of a polygon.

Note: The name of the polygon is termed according to the number of sides it has. For Example, if N= number of sides of polygon, then:
N=5 (Polygon is called pentagon)
N=6 (Polygon is called hexagon)
N=7 (Heptagon)
N=8 (Octagon)
N=9 (nonagon)
Regular polygon: Polygon in which all the sides and interior angles are equal are known as Regular polygon.
Irregular Polygon: Polygon in which all the sides and interior angles are not equal are known as Irregular polygon.