Question

The sum of angles of quadrilateral is
A.${{180}^{\circ }}$
B. ${{360}^{\circ }}$
C. ${{270}^{\circ }}$
D. none of these

Answer 1

Hint: We recall the shape of a quadrilateral, the definition of internal angles, and the interior angle sum theorem which states that the sum of the internal angles of a polygon with $n$ sides is given by $\left( n-2 \right){{180}^{\circ }}$. We use this formula to find the sum of angles of a quadrilateral which has 4 sides.

Complete step by step answer:
We know that a polygon is a simple closed curve made up of line segments. The line segments are called sides of the polygon and the points of joints of sides are called vertices. The angle subtended by two sides at the shared vertex in the interior of the polygon is called the internal angle or the interior angle of the polygon. If there are $n$ sides of the polygon, there are $n$ internal angles. The sum of measures of all the angles of a polygon is given by $\left( n-2 \right){{180}^{\circ }}$.
We know that quadrilateral is a polygon with 4 sides and 4 vertices. We name quadrilateral with four vertices, for example, ABCD.

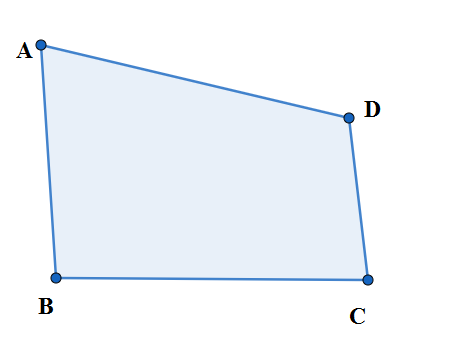
So the four internal angles of the quadrilateral are $\angle ABC,\angle BCD,\angle CDA,\angle DAB$. So the sum of measures of internal angles by the formula for sum of the angles is
\[\left( n-2 \right){{180}^{\circ }}=\left( 4-2 \right){{180}^{\circ }}=2\times {{180}^{\circ }}={{360}^{\circ }}\]
So we have;
\[\angle ABC+\angle BCD+\angle CDA+\angle DAB={{360}^{\circ }}\]
Hence the correct option is C.
Note:
We note that the sum of the angles without mentioned is the sum of internal angles. The external angles are angles subtended at the vertex by a side and an extended adjacent side. The sum of external angles is ${{360}^{\circ }}$ irrespective of the number of sides. We have drawn the figure of a convex quadrilateral. We note that the sum of the angles does not change for the concave quadrilateral.