Question

The square on the diagonal of a cube has an area of 1875 sq.cm. Calculate the total surface area of the cube.

Answer 1

Hint: The length of the diagonal of the cube of side \[a{\text{ cm}}\] is given by \[l = a\sqrt 3 \]cm. The side of the square is equal to the length of diagonal of the cube. The area of the square of \[x{\text{ cm}}\] is given by \[{x^2}{\text{ c}}{{\text{m}}^2}\]. The total surface of the cube with side \[a{\text{ cm}}\] is given by \[6{a^2}{\text{ c}}{{\text{m}}^2}\]. So, use this concept to reach the solution of the problem.

Complete step-by-step answer:
Let the side of the cube be \[a{\text{ cm}}\]
We know that the length of the diagonal of the cube of side \[a{\text{ cm}}\] is given by \[l = a\sqrt 3 \]cm.
Therefore, the length of the diagonal of the given cube is \[a\sqrt 3 {\text{ cm}}\]
The diagram of square on the diagonal of the cube is given below:

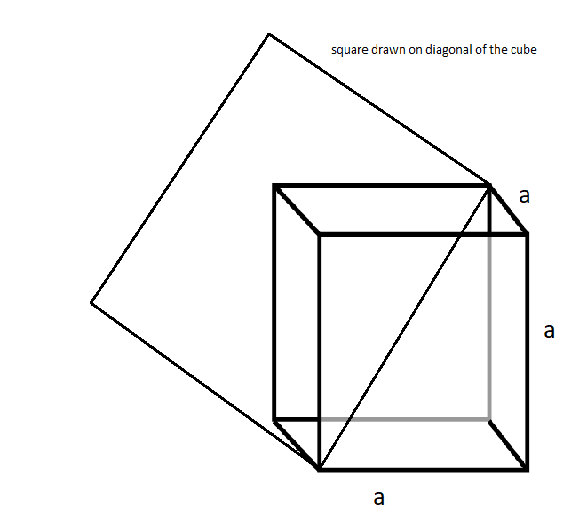
We know that the area of the square of \[x{\text{ cm}}\] is given by \[{x^2}{\text{ c}}{{\text{m}}^2}\].
So, the area of the square drawn on the diagonal of the cube \[ = {\left( {a\sqrt 3 } \right)^2} = 3{a^2}{\text{ c}}{{\text{m}}^2}\]
But given that the square on the diagonal of a cube has an area of 1875 sq.cm.
By equating them, we have
\[
   \Rightarrow 3{a^2} = 1875 \\
   \Rightarrow {a^2} = \dfrac{{1875}}{3} \\
   \Rightarrow {a^2} = 625 \\
  \therefore a = 25{\text{ cm}} \\
\]
Total surface of the cube with side \[a{\text{ cm}}\] is given by \[6{a^2}{\text{ c}}{{\text{m}}^2}\]
So, the total surface area of the cube \[ = 6{\left( {25} \right)^2} = 6\left( {625} \right) = 3750{\text{ c}}{{\text{m}}^2}\]
Thus, the total surface area of the cube is 3750 sq.cm.

Note: Here we have not considered \[a = - 25{\text{ cm}}\] as the side of the cube cannot be negative. The units of total surface area can be written as sq.cm or \[{\text{c}}{{\text{m}}^2}\]. The main diagonal of a cube is the one that cuts through the centre of the cube; the diagonal of the face of a cube is not the main diagonal.