
The slope of any line which is parallel to x-axis is …………. .
A.0
B.1
C.-1
D.2
Answer
611.4k+ views
Hint: In this question we are asked to find the slope of a straight line which is parallel to x-axis. But, here we didn’t get any coordinates or equations in the question. So, we will try to find it by drawing a straight line on the graph and find the slope by using formula of $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ to get the answer.
Complete step-by-step answer:
Here, we need to find the slope of any line which is parallel to x-axis.
Let us draw a straight line AB on the graph which is parallel to x-axis.
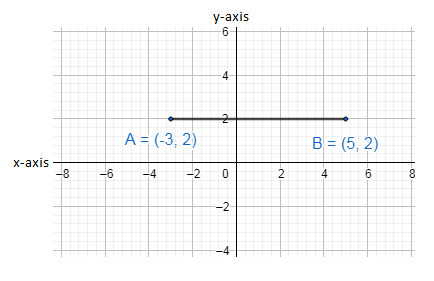
In this graph, the horizontal line is x-axis and the vertical line is y-axis.
By drawing the straight line on the graph we get two points A and B where $\left( {{x}_{1}},{{y}_{1}} \right)$is A$\left( -3,2 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$is B$\left( 5,2 \right)$ .
Now, we can find the slope of the straight line parallel to the x-axis by taking A and B in the formula of slope.
i.e. $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.
Put, $A=\left( {{x}_{1}},{{y}_{1}} \right)=\left( -3,2 \right)$ and $B=\left( {{x}_{2}},{{y}_{2}} \right)=\left( 5,2 \right)$
$\begin{align}
& \text{slope}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \\
& =\dfrac{2-2}{5-\left( -3 \right)} \\
& =\dfrac{0}{8} \\
& =0 \\
\end{align}$
By this we get to know that the slope of any straight line parallel to the x-axis is 0.
Therefore, option (a) is the correct answer.
Note: Generally students get confused while solving such types of questions and they may make mistakes while taking x and y coordinates. They should know that y coordinates of the straight line parallel to x-axis will always be the same. Students can solve this problem logically. The slope of a straight line parallel to the x-axis will always be ‘0’ as there will be no slope to the straight line which is parallel to the axis.
Complete step-by-step answer:
Here, we need to find the slope of any line which is parallel to x-axis.
Let us draw a straight line AB on the graph which is parallel to x-axis.
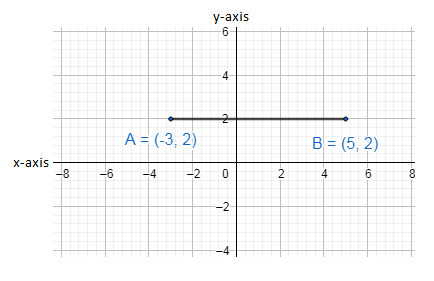
In this graph, the horizontal line is x-axis and the vertical line is y-axis.
By drawing the straight line on the graph we get two points A and B where $\left( {{x}_{1}},{{y}_{1}} \right)$is A$\left( -3,2 \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$is B$\left( 5,2 \right)$ .
Now, we can find the slope of the straight line parallel to the x-axis by taking A and B in the formula of slope.
i.e. $\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$.
Put, $A=\left( {{x}_{1}},{{y}_{1}} \right)=\left( -3,2 \right)$ and $B=\left( {{x}_{2}},{{y}_{2}} \right)=\left( 5,2 \right)$
$\begin{align}
& \text{slope}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \\
& =\dfrac{2-2}{5-\left( -3 \right)} \\
& =\dfrac{0}{8} \\
& =0 \\
\end{align}$
By this we get to know that the slope of any straight line parallel to the x-axis is 0.
Therefore, option (a) is the correct answer.
Note: Generally students get confused while solving such types of questions and they may make mistakes while taking x and y coordinates. They should know that y coordinates of the straight line parallel to x-axis will always be the same. Students can solve this problem logically. The slope of a straight line parallel to the x-axis will always be ‘0’ as there will be no slope to the straight line which is parallel to the axis.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

Name the part of the brain responsible for the precision class 11 biology CBSE

The growth of tendril in pea plants is due to AEffect class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




