Question

The slope of a chord of the parabola ${{y}^{2}}=4ax$, which is normal at one end and which subtends a right angle at the origin, is
(a)$1/\sqrt{2}$
(b)$\sqrt{2}$
(c)2
(d)None of these

Answer 1

Hint: Suppose two points of the normal chord lying on parabola as $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right),\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$. Get the slope of the tangent at the point where the chord acts as a normal for parabola, by differentiating the curve ${{y}^{2}}=4ax$at that point. Hence, get the slope of normal using relation.

Complete step-by-step answer:
Product of slopes of two perpendicular lines = -1. Get the slope of chord using the coordinates supposed as well with the help of relation = $\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)$
Where \[\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)\] are lying on the line. And use the given condition to solve the problem further.

As, we need to find the slope of a chord in ${{y}^{2}}=4ax$, which is normal at one end and subtends a right angle at the origin as well. So, let the two ends of the chord are $\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right),\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)$
[parametric coordinates for ${{y}^{2}}=4ax$].
So, diagram can be represented as

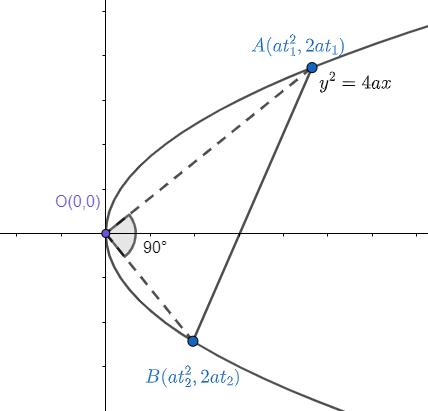
Let AB is acting as a normal at the point B.
We know the slope of tangent at point B can be given
${{\left. \dfrac{dy}{dx} \right|}_{\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)}}$ …………..(i)
Where, we need to use relation
${{y}^{2}}=4ax$
So, differentiating ${{y}^{2}}=4ax$,
We get
$\begin{align}
  & \dfrac{d}{dx}{{y}^{2}}=\dfrac{d}{dx}\left( 4ax \right) \\
 & 2y\dfrac{dy}{dx}=4a\times 1 \\
\end{align}$
Where, we know
$\dfrac{d}{dx}{{x}^{n}}=n{{x}^{n-1}}$
Hence, we get
$\begin{align}
  & y\dfrac{dy}{dx}=2a \\
 & \dfrac{dy}{dx}=\dfrac{2a}{y} \\
\end{align}$
Now, we can get slope of tangent at point B as
${{\left. \dfrac{dy}{dx} \right|}_{\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right)}}=\dfrac{2a}{2a{{t}_{2}}}=\dfrac{1}{{{t}_{2}}}$………………(ii)
Now, we know tangent is perpendicular to the normal at the point of tangency for any conic. And as, we know the relation between slopes of two perpendicular lines is given as
Product of two perpendicular lines = -1…………..(iii)
So, we get
\[\begin{align}
  & \text{slope of normal at B }\times \text{ slope of tangent at B = -1} \\
 & \dfrac{\text{1}}{{{\text{t}}_{\text{2}}}}\text{ }\!\!\times\!\!\text{ slope of normal at B = -1} \\
 & \text{slope of normal at B = -}{{\text{t}}_{\text{2}}} \\
\end{align}\]
Now, we can calculate slope of normal at B i.e. slope of line AB by formula
$\text{slope = }\dfrac{{{\text{y}}_{\text{2}}}\text{ - }{{\text{y}}_{\text{1}}}}{{{\text{x}}_{\text{2}}}\text{ - }{{\text{x}}_{\text{1}}}}$ ………………..(iv)
So, we get
$\begin{align}
  & \text{slope of normal at B = }\dfrac{\text{2a}{{\text{t}}_{\text{2}}}\text{-2a}{{\text{t}}_{\text{1}}}}{\text{a}{{\text{t}}_{\text{2}}}^{\text{2}}\text{-a}{{\text{t}}_{\text{1}}}^{\text{2}}} \\
 & =\dfrac{2a\left( {{t}_{2}}-{{t}_{1}} \right)}{a\left( {{t}_{2}}^{2}-{{t}_{1}}^{2} \right)} \\
 & =\dfrac{2\left( {{t}_{2}}-{{t}_{1}} \right)}{\left( {{t}_{1}}+{{t}_{2}} \right)\left( {{t}_{2}}-{{t}_{1}} \right)} \\
\end{align}$
$\text{slope of normal at B = }\dfrac{\text{2}}{{{\text{t}}_{\text{1}}}\text{+}{{\text{t}}_{\text{2}}}}$
As, we have already calculated the slope of normal at point B $\to -{{t}_{2}}$. So, we get
\[\begin{align}
  & \dfrac{2}{{{t}_{1}}+{{t}_{2}}}=-{{t}_{2}} \\
 & -2={{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right) \\
\end{align}\]
\[{{t}_{1}}+{{t}_{2}}+{{t}_{2}}^{2}=-2\]…………(v)
Now, as AO and BO are perpendicular to each other. So, we can calculate the slopes of them and use equation (iii).
So, we get slope of AO from the equation (iv) as
$\begin{align}
  & \text{slope of AO = }\dfrac{\text{2a}{{\text{t}}_{\text{1}}}\text{-0}}{\text{a}{{\text{t}}_{\text{1}}}^{\text{2}}\text{-0}}\text{=}\dfrac{\text{2a}{{\text{t}}_{\text{1}}}}{\text{a}{{\text{t}}_{\text{1}}}^{\text{2}}} \\
 & \text{slope of AO = }\dfrac{\text{2}}{{{\text{t}}_{\text{1}}}} \\
\end{align}$
Similarly, slope of $BO=\dfrac{2}{{{t}_{2}}}$
Now, using equation (iii), we get
$\begin{align}
  & \dfrac{2}{{{t}_{1}}}\times \dfrac{2}{{{t}_{2}}}=-1 \\
 & 4=-{{t}_{1}}{{t}_{2}}, \\
\end{align}$
${{t}_{1}}{{t}_{2}}=-4$…………….(vi)
Putting ${{t}_{1}}{{t}_{2}}=-4$in equation (vi), we get (v), we get
\[\begin{align}
  & -4+{{t}_{2}}^{2}=-2 \\
 & {{t}_{2}}^{2}=4-2=2 \\
 & {{t}_{2}}=\pm \sqrt{2} \\
\end{align}\]
Putting ${{t}_{2}}=\pm \sqrt{2}$in equation (vi), we get
Case 1:
$\begin{align}
  & {{t}_{2}}=\sqrt{2} \\
 & {{t}_{1}}\times \sqrt{2}=-4 \\
 & {{t}_{1}}=\dfrac{-4}{\sqrt{2}}\times \dfrac{\sqrt{2}}{\sqrt{2}}=-2\sqrt{2} \\
\end{align}$
Case 2:
$\begin{align}
  & {{t}_{2}}=-\sqrt{2} \\
 & {{t}_{1}}\times -\sqrt{2}=-4 \\
 & {{t}_{1}}=\dfrac{-4}{-\sqrt{2}}=\dfrac{4}{\sqrt{2}}\times \dfrac{\sqrt{2}}{\sqrt{2}}=2\sqrt{2} \\
 & {{t}_{1}}=2\sqrt{2} \\
\end{align}$
Hence, slope of normal at B is given as $\dfrac{2}{{{t}_{1}}+{{t}_{2}}}$
Case 1:
Put ${{t}_{1}}=2\sqrt{2},{{t}_{2}}=-\sqrt{2}$
Slope of chord = $\begin{align}
  & \dfrac{2}{2\sqrt{2}-\sqrt{2}}=\dfrac{2}{\sqrt{2}}\times \dfrac{\sqrt{2}}{\sqrt{2}} \\
 & =\sqrt{2} \\
\end{align}$
Case 2:
Put ${{t}_{1}}=-2\sqrt{2},{{t}_{2}}=\sqrt{2}$
Slope of chord = $\dfrac{2}{{{t}_{1}}+{{t}_{2}}}$
\[=\dfrac{2}{-2\sqrt{2}+\sqrt{2}}=\dfrac{2}{-\sqrt{2}}\times \dfrac{\sqrt{2}}{\sqrt{2}}\]
Slope of chord = -\[\sqrt{2}\]
Hence, there are two possibilities of slope of chord for the given condition in the problem;
\[-\sqrt{2},\sqrt{2}\]
Hence, option (b) is the correct answer.
Note: One may use points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ as well for representing the point A and B and need to use two more equations, that are ${{y}_{1}}^{2}=4a{{x}_{1}},{{y}_{2}}^{2}=4a{{x}_{2}}$. So, it can be another approach. But involvement of two more equations, may make the problem complex for some of the students. So, always try to use parametric form of coordinates in this kind of problems.
We can use another approach to get the slope of the normal at any conic as well. We can write the equation of tangent at point A and B by using equation
T = 0
i.e. replace
 $\begin{align}
  & {{x}^{2}}\to x{{x}_{1}} \\
 & {{y}^{2}}\to y{{y}_{1}} \\
 & x\to \dfrac{x+{{x}_{1}}}{2} \\
 & y\to \dfrac{y+{{y}_{1}}}{2} \\
\end{align}$
Where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the point on the given conic. Hence, compare the calculated equation of tangent with the line y = mx + c to get slope of tangent and hence, get slope of normal by relation
Product of slopes of two perpendicular lines = -1