Question

The side of a square based prism is \[2.5\]cm and its height is \[6.5\]cm. Find its lateral and total surface area.

Answer 1

Hint:To find the lateral surface area we multiply the area of the triangle of the prism four times as:

Lateral surface area \[=\text{ }4\text{ }\times \] Area of the triangles
And to find the total surface area of the prism we can add the area of the base of the prism by the area of the lateral surface area as:

Total Surface Area = Area of the base of the prism\[+\text{ }4\times \]Area of face of a triangle.

Complete step by step solution:
To calculate the lateral surface area we need the area of the triangle. Now to calculate the area of the triangle we will check the diagram given below:

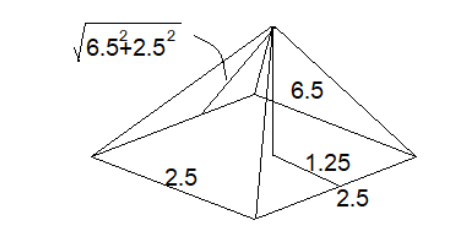
To calculate the area we need the slant height of the prism and the value of that height is:
\[\Rightarrow {{6.5}^{2}}+{{\left( \dfrac{2.5}{2} \right)}^{2}}\]
\[\Rightarrow \sqrt{42.25+1.56}\]

\[\Rightarrow 6.61\] cm

With the value of the slant height and base of the triangle we get the area of each triangle as:
\[\Rightarrow \dfrac{6.61\times 2.5}{2}\]
\[\Rightarrow 8.26\text{ }c{{m}^{2}}\]

Now let us move on the lateral surface area value of the prism, the value of the lateral surface area of the prism is formed by the product of the area of the triangle by \[4\].

Placing the value of the area of the triangles we get the lateral surface area as:
P \[=\text{ }4\text{ }\times \text{ }8.26\text{ }=\text{ }33.05\text{ }c{{m}^{2}}\]

With the lateral surface area found, the value of the total surface area of the prism is calculated by the formula of

Total Surface Area = Area of the base of the prism\[+\text{ }4\times \]Area of face of a triangle.

Placing the value of area of triangle as:
\[\Rightarrow 8.26\text{ }c{{m}^{2}}\]
And the value of area of the square as:
\[\Rightarrow 2.5\text{ }cm\times 2.5\text{ }cm\]
\[\Rightarrow 6.25\text{ }c{{m}^{2}}\]

Now adding both of them we get the value of the total surface area as:

Total Surface Area = \[6.25+4\times 8.26\]
\[\Rightarrow 6.25+33.04\]
\[\Rightarrow 39.29\text{ }c{{m}^{2}}\]

Therefore, the value of the lateral surface area is and the value of the total surface area of the prism is given as \[33.05\text{ }c{{m}^{2}}\] and \[39.29\text{ }c{{m}^{2}}\].

Note:The lateral surface area of an object is the total sum of the areas of an object minus the top and the bottom and in case of a prism the top is a point with negligible area and base with a square surface. Now we can also use the formula of lateral surface area of the pyramid as well maintain that both length and width of the prism are same as:

\[{{A}_{lateral}}=l\sqrt{{{\left( \dfrac{w}{2} \right)}^{2}}+{{h}^{2}}}+w\sqrt{{{\left( \dfrac{l}{2}
\right)}^{2}}+{{h}^{2}}}\].