Question

The SI unit of solid angle is
A. radians
B. steradians
C. degrees
D. All of the above

Answer 1

Hint: Making a 3D diagram, with a solid angle will help in understanding how to find a solid angle. That will help in eliminating few of the options. Knowing the SI units of length , angles etc. is also necessary.

Complete step-by-step answer:
Let’s start by the definition of a solid angle. In general, solid angle is the 3-dimensional angle subtended by any object in 3-dimensional space. To easily understand, it’s the cone subtended by a 2-dimensional object with respect to a point. Seeing the diagram below will help in understanding further.

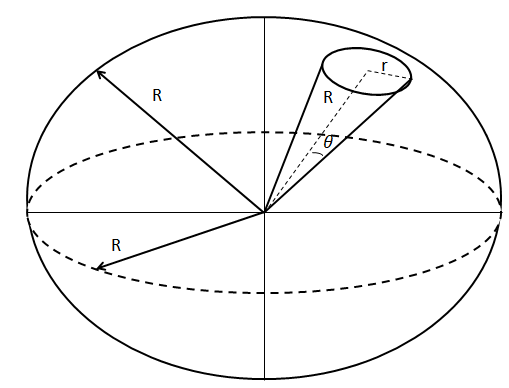
Here, we are taking the example of a sphere as the 3D surface and the area of the cone is the object whose solid angle we will try to find out.
The formula of the solid angle$(\Omega )$ is, $\Omega =$Area of part of the spherical surface subtended divided by the radius of the area of the part of the spherical surface subtended. That is, $\Omega =\dfrac{A}{{{r}^{2}}}.$
The area is $4\pi {{r}^{2}}$ $\therefore \Omega =\dfrac{4\pi {{r}^{2}}}{{{r}^{2}}}=4\pi $steradians.
The general formula for the same would be, $d\Omega =\dfrac{dA}{{{r}^{2}}}=\dfrac{(r\sin \theta d\phi )(rd\theta )}{{{r}^{2}}}=\sin \theta d\theta d\phi $
$\therefore \Omega =\int{\int{\sin \theta d\theta d\phi }}$
For the case that we have taken as an example, $\Omega =\int{\int{\sin \theta d\theta d\phi }}\Rightarrow \Omega =\int\limits_{0}^{2\pi }{d\phi }\int\limits_{0}^{\pi }{\sin \theta d\theta }\Rightarrow \Omega =4\pi $steradians.

Note: It’s important the physical significance of solid angle, the solid angle is necessary to understand how an object can look bigger as it moves further away from the apex of the cone and how the object looks smaller as it comes closer to the apex of the cone. Since, the solid angle is the ratio of the object's surface area (part of the area of the sphere) with respect to the square of the radius of the area of the part of the sphere, hence, for the ratio to be constant, the following proportionality will hold. \[Area\propto {{r}^{2}}\]
Also another important point to remember would be that, like the 2-D angle having units of degrees or radians, the 3-D solid angle having units of steradians is also dimensionless.