Question

The shortest distance from (– 2, 14) to the circle \[{{x}^{2}}+{{y}^{2}}-6x-4y-12=0\] is:
(a) 4
(b) 6
(c) 8
(d) 10

Answer 1

Hint: First of all, consider the point (– 2, 14) as P and plot the given circle and point P on the coordinate plane. Now find the shortest distance by using (PO – r) where O is the center and r is the radius of the circle.

Complete step-by-step solution:
In this question, we have to find the shortest distance from (– 2, 14) to the circle \[{{x}^{2}}+{{y}^{2}}-6x-4y-12=0.\] Let us first name the given point as P, so, we get the point as P (– 2, 14). Now, let us consider our circle C.
\[C:{{x}^{2}}+{{y}^{2}}-6x-4y-12=0\]
Let us rearrange the terms of this equation.
\[\Rightarrow C:{{x}^{2}}-6x+{{y}^{2}}-4y-12=0\]
\[\Rightarrow C:{{x}^{2}}-2\times 3\times x+{{y}^{2}}-2\times 2y-12=0\]
\[\Rightarrow C:{{x}^{2}}-2\times 3\times x+{{\left( 3 \right)}^{2}}-{{\left( 3 \right)}^{2}}+{{y}^{2}}-2\times 2y+{{\left( 2 \right)}^{2}}-{{\left( 2 \right)}^{2}}-12=0\]
We know that \[{{a}^{2}}-2ab+{{b}^{2}}={{\left( a-b \right)}^{2}}.\] By using this in the above equation, we get,
\[\Rightarrow C:{{\left( x-3 \right)}^{2}}-{{\left( 3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}-{{\left( 2 \right)}^{2}}-12=0\]
By further simplifying the above equation, we get,
\[\Rightarrow C:{{\left( x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}=9+4+12\]
\[\Rightarrow C:{{\left( x-3 \right)}^{2}}+{{\left( y-2 \right)}^{2}}={{\left( 5 \right)}^{2}}\]
As we know that the general equation of the circle is \[{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}\] where \[\left( {{x}_{1}},{{y}_{1}} \right)\] is the centre of the circle and r is the radius of the circle.
By using this, we get the center of circle C as O (3, 2) and the radius of the circle C as ‘r’ = 5 units. Let us draw the circle C and point P on the coordinate plane using the above information.

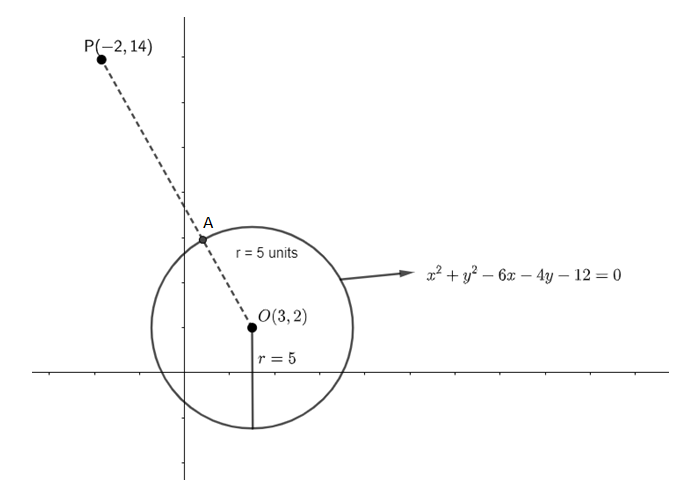
From the above figure, we can see that the shortest distance is PA and from the figure, we get, PA = PO – OA. We know that OA is nothing but the radius of the circle. So, we get,
\[\Rightarrow PA=PO-r\]
We have found that r = 5, so we get,
\[\Rightarrow PA=PO-5.....\left( i \right)\]
Let us find the value of the PO. We know that P = (– 2, 14) and O = (3, 2). By using the distance formula that is, \[d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}},\] we get the distance between P and O as
\[PO=\sqrt{{{\left( -2-3 \right)}^{2}}+{{\left( 14-2 \right)}^{2}}}\]
\[\Rightarrow PO=\sqrt{{{\left( -5 \right)}^{2}}+{{\left( 12 \right)}^{2}}}\]
\[\Rightarrow PO=\sqrt{25+144}\]
\[\Rightarrow PO=\sqrt{169}\]
\[\Rightarrow PO=13\text{ units}\]
By substituting the value of PO in the equation (i), we get,
\[\Rightarrow PA=13-5=8\text{ units}\]
Hence, we get the shortest distance from (– 2, 14) to the circle \[{{x}^{2}}+{{y}^{2}}-6x-4y-12=0\] as 8 units.
Therefore, option (c) is the right answer.

Note: Students should remember that if the point P is lying outside the given circle, then the shortest distance between point P and the circle is (PO – r) whereas when point P is lying inside the circle then the shortest distance is (r – PO) where r is the radius of the given circle and PO is the distance between the given point and the center of the circle. We can find if the point P is lying outside or inside of the circle by substituting the x and y coordinates of the point in the circle. After simplifying it, if the value comes to be negative, then the point is lying inside, if it is positive, then the point is lying outside and if it is 0, then the point is lying on the circle. So, we need not draw the circle every time.