Question

The shortest distance a spider should crawl from one corner to the opposite corner of a cubical room of dimensions 3m is
(A) $ 3\sqrt 3 m $
(B) $ \left( {3\sqrt 2 + 3} \right)m $
(C) $ 3\sqrt 5 m $
(D) 9m

Answer 1

Hint
In a cubical room the shortest distance is along one of the diagonals. But the diagonal joining one corner of the room to the opposite corner gives an aerial route and the spider can only crawl. So we need to open up the cubical room in 2 dimensions and then find the shortest distance.
To solve this question we will be using the following formulas,
In a right angle triangle,
$\Rightarrow H = \sqrt {{B^2} + {P^2}} $
Where $ H $ is the hypotenuse, $ B $ is the base, and $ P $ is the perpendicular of the triangle.

Complete step by step answer
For solving this question, we need to first draw the diagram of what the room looks like if we flatten out the walls. This is because the spider can only crawl, so we need to draw the cubical room in 2 dimensions.

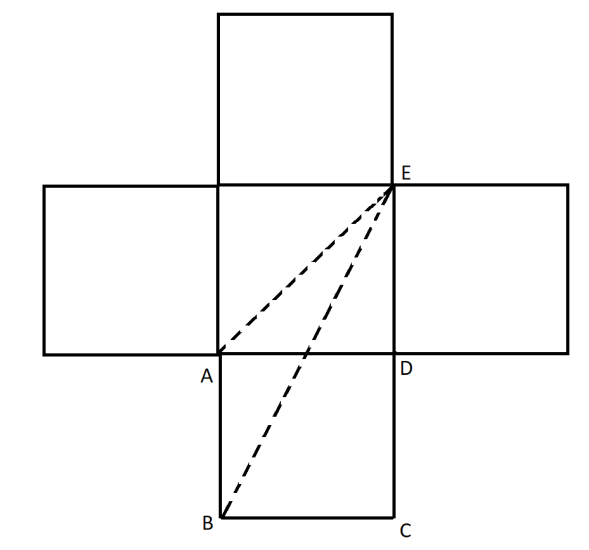
Here as we can see the line BE gives the diagonal of the room. While the room was in 3D, the diagonal could be found out by,
$\Rightarrow BE = \sqrt {{{\left( {AE} \right)}^2} + {{\left( {AB} \right)}^2}} $
But this diagonal though is the shortest distance but still runs through the middle of the room. This means that this diagonal covers the distance through the air. But the spider can only crawl on the walls. So the spider can’t take this path.
Now from the figure, we can see that the line BE is the shortest distance. So we can find the length of BE from the triangle BCE. In that triangle, BE is the hypotenuse. So we can find BE by the formula,
$\Rightarrow BE = \sqrt {{{\left( {BC} \right)}^2} + {{\left( {CE} \right)}^2}} $
Now, in the question, the dimensions of the room are given to be 3m. So the length of BC is 3m and the length of CE can be divided into 2 parts as,
$\Rightarrow CE = CD + DE $
and the values of CD and DE are 3m each. So the value of CE is,
$\Rightarrow CE = 3 + 3 = 6m $
So by substituting the values of BC and CE in the equation of BE we get,
$\Rightarrow BE = \sqrt {{{\left( 3 \right)}^2} + {{\left( 6 \right)}^2}} $
So on doing the squares we get,
$\Rightarrow BE = \sqrt {9 + 36} $
Therefore we get the value of BE as,
$\Rightarrow BE = \sqrt {45} m $
We can write this as,
$\Rightarrow BE = \sqrt {3 \times 3 \times 5} m $
So the 3 comes out of the root and we get,
$\Rightarrow BE = 3\sqrt 5 m $
So the shortest distance for the spider to crawl is $ 3\sqrt 5 m $.
Hence, the correct answer is option (C). $ 3\sqrt 5 m $ .

Note
The spider could have also taken the route from B to E as BA and then AE. Then the distance covered by the spider would have been, $ BA + AE $ . The value of BA is 3m and the value of AE is-
$\Rightarrow AE = \sqrt {{{\left( 3 \right)}^2} + {{\left( 3 \right)}^2}} $
So the value of $ AE = \sqrt {18} = 3\sqrt 2 m $.
Therefore we get the distance covered by the spider as, $ \left( {3\sqrt 2 + 3} \right)m $ which is greater than $ 3\sqrt 5 m $ . So it is not the shortest distance.