Question

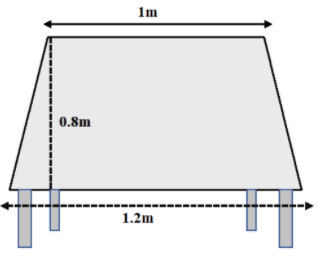
The shape of the top surface of a table is a trapezium. Find its area if it’s parallel sides are 1m and 1.2m and the perpendicular distance between them is 0.8m.

Answer 1

Hint: We are given that the lengths of the parallel sides of a trapezium are 1m and 1.2m, and the distance between two parallel lines is 0.8m. Substitute the values in the formula of area of trapezium, $A = \dfrac{1}{2}\left( {a + b} \right)h$, where $a$ and $b$ are length of parallel lines and $h$ is the distance between parallel lines.

Complete step by step solution: We have to find the area of the top surface of the table.
The shape of the tabletop is a trapezium.
We are given that the lengths of the parallel sides of a trapezium are 1m and 1.2m, and the distance between two parallel lines is 0.8m
We know that the area of the trapezium is half the product of distance between parallel lines and the sum of the length of parallel lines.
That is, $A = \dfrac{1}{2}\left( {a + b} \right)h$, where $a$ and $b$ are length of parallel lines and $h$ is the distance between parallel lines.
On substituting $a = 1$, $b = 1.2$ and $h = 0.8$ in the above formula of area of the trapezium, we will get,
$A = \dfrac{1}{2}\left( {1 + 1.2} \right)\left( {0.8} \right)$
On solving the brackets, we will get,
$A = \dfrac{1}{2}\left( {2.2} \right)\left( {0.8} \right)$
Multiply the brackets,
$A = \dfrac{1}{2}\left( {1.76} \right)$
Now, on dividing by 2, we will get,
$A = 0.88{m^2}$

Hence, the area of the tabletop is $0.88\;{m^2}$


Note: A trapezium is a quadrilateral with a pair of parallel sides and a pair of non-parallel sides. Perimeter is the summation of lengths of all sides of the trapezium. And the area of the trapezium is the $\dfrac{1}{2}\left( {a + b} \right)h$, where $a$ and $b$ are length of parallel lines and $h$ is the distance between parallel lines. The area of any figure is always measured in square units.