
The shadow of a vertical tower on level ground increases by 10 metre when the altitude of the sun changes from the angle of elevation 45° to 30°. Find the height of the tower correct to one place of decimal. (take $\sqrt 3 $=1.732)
A) 13.67 m
B) 15 m
C) 18.67 m
D) 20 m

Answer
575.4k+ views
Hint:
We need to calculate the value of h in the given figure. For that, we will first calculate the value of x in terms of h using the trigonometric formula of tan $\theta $= $\dfrac{{perpendicular}}{{base}}$in the triangle BCD. And, after that, we will apply the trigonometric formula of tan $\theta $in the triangle ACD to calculate the value of h. After putting the value of $\sqrt 3 $, we will get the value of h.
Complete step by step solution:
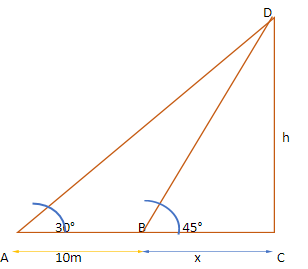
Let us assume the height of the tower be h.
Let us look at the figure:
In the triangle BCD, we have
tan 45° = $\dfrac{{perpendicular}}{{base}}$= $\dfrac{h}{x}$
$
\Rightarrow 1 = \dfrac{h}{x} \\
\Rightarrow x = h \\
$
Now, in the triangle ACD, we have
tan 30° = $\dfrac{{perpendicular}}{{base}}$= $\dfrac{h}{{x + 10}}$
$ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{x + 10}}$
On putting the value x = h in the above equation and solving for h, we get
\[
\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{h + 10}} \\
\Rightarrow \sqrt 3 h = h + 10 \\
\Rightarrow \left( {\sqrt 3 - 1} \right)h = 10 \\
\]
Substituting the value of $\sqrt 3 $as given in the question as 1.732, we get
$
\Rightarrow \left( {1.732 - 1} \right)h = 10 \\
\Rightarrow h = \dfrac{{10}}{{0.732}} \\
\Rightarrow h = 13.67 \\
$
Hence, the height of the tower is 13.67m.
Therefore, option(A) is correct.
Note:
Many students have misconceptions about height and distance problems that always tan are applied to problems in this chapter. We always recommend not to have such misconceptions. read the question draw the diagram then depending on the need we use trigonometric ratios.
We need to calculate the value of h in the given figure. For that, we will first calculate the value of x in terms of h using the trigonometric formula of tan $\theta $= $\dfrac{{perpendicular}}{{base}}$in the triangle BCD. And, after that, we will apply the trigonometric formula of tan $\theta $in the triangle ACD to calculate the value of h. After putting the value of $\sqrt 3 $, we will get the value of h.
Complete step by step solution:
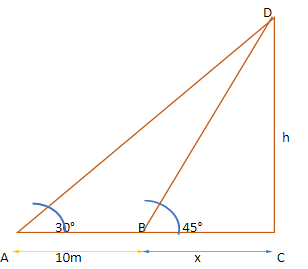
Let us assume the height of the tower be h.
Let us look at the figure:

In the triangle BCD, we have
tan 45° = $\dfrac{{perpendicular}}{{base}}$= $\dfrac{h}{x}$
$
\Rightarrow 1 = \dfrac{h}{x} \\
\Rightarrow x = h \\
$
Now, in the triangle ACD, we have
tan 30° = $\dfrac{{perpendicular}}{{base}}$= $\dfrac{h}{{x + 10}}$
$ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{x + 10}}$
On putting the value x = h in the above equation and solving for h, we get
\[
\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{h + 10}} \\
\Rightarrow \sqrt 3 h = h + 10 \\
\Rightarrow \left( {\sqrt 3 - 1} \right)h = 10 \\
\]
Substituting the value of $\sqrt 3 $as given in the question as 1.732, we get
$
\Rightarrow \left( {1.732 - 1} \right)h = 10 \\
\Rightarrow h = \dfrac{{10}}{{0.732}} \\
\Rightarrow h = 13.67 \\
$
Hence, the height of the tower is 13.67m.
Therefore, option(A) is correct.
Note:
Many students have misconceptions about height and distance problems that always tan are applied to problems in this chapter. We always recommend not to have such misconceptions. read the question draw the diagram then depending on the need we use trigonometric ratios.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE




