Question

The shadow of a stick of height 1 metre, when the angle of elevation of the sun is 60, will be
(A) $\dfrac{1}{\sqrt{3}}m$
(B) $\dfrac{1}{3}m$
(C) $\sqrt{3}m$
(D) $3m$

Answer 1

Hint: We start solving this problem by first understanding that the angle of elevation of the Sun is the same as the angle of elevation of the stick with the shadow of the stick. Then we draw a diagram from the information given. Then we consider the tangent of the angle of elevation, using the formula $\tan \theta =\dfrac{\text{Base}}{\text{Opposite}}$ and substitute the value of length of stick and solve it to find the length of the shadow of the stick.

Complete step-by-step answer:
We are given that the length of the stick is 1 metre. We are also given that the angle of elevation of the sun is ${{60}^{\circ }}$.
The length of the shadow is based on the angle of the elevation of the Sun.
So, the angle of elevation of Sun is equal to the angle of elevation of the stick.
Let us assume that the length of the shadow of the stick as h metres. Let the PQ be stick which is 1m. Then the shadow is QR.

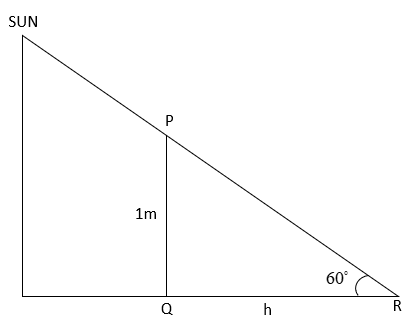
Now let us consider the triangle PQR. Then we can see that in that triangle,
$\tan {{60}^{\circ }}=\dfrac{PQ}{QR}$
Now, let us substitute the value of PQ, which is the length of the stick, that is 1m. So, we get
$\begin{align}
  & \Rightarrow \sqrt{3}=\dfrac{1}{QR} \\
 & \Rightarrow QR=\dfrac{1}{\sqrt{3}} \\
\end{align}$
So, we get that the length of the shadow is $\dfrac{1}{\sqrt{3}}$m.

So, the correct answer is “Option A”.

Note: The common mistake one makes while solving this problem is one might take the trigonometric ratios wrong like $\tan {{60}^{\circ }}=\dfrac{1}{\sqrt{3}}$. If one makes that mistake then we get,
$\begin{align}
  & \Rightarrow \tan {{60}^{\circ }}=\dfrac{1}{\sqrt{3}}=\dfrac{1}{QR} \\
 & \Rightarrow QR=\sqrt{3} \\
\end{align}$
So, one might make this mistake and mark the answer as Option C. So, one needs to remember the trigonometric ratios correctly.